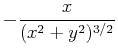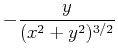質量Mの太陽が原点にあり,質量mの惑星の位置がx,yで示されるとき,惑星の運動方程式は以下のようにかける.
ここでGMm=1とした.,ルンゲクッタ法のプログラムにするために速度と位置の連立微分方程式とする.
dx/dt = vx,
dy/dt = vy
と
dvx/dt = -x/(x**2+y**2)**1.5D0,
dvy/dt = -y/(x**2+y**2)**1.5D0
の4元連立微分方程式となる.
練習問題1
先週の課題を参考に,太陽からの重力を受ける惑星の運動をルンゲクッタ法で解くプログラムを作成せよ.
座標として用いる変数はx,yとし,速度はvx, vyとすること.座標の変化分を与える関数をdxdt, dydt,速度の変化分を与える関数をdvxdt, dvydt とすること.なので関数の宣言とプログラムの主要部分は概ね次のようになる.具体的な関数の中身は式(1)を参考にすること.
double precision function dxdt(t, x, y, vx, vy) ! 関数の定義:xの増分
implicit none
.....
double pcecision function dvxdt(t, x, y, vx, vy) ! 関数の定義:vxの増分
implicit none
.....
dx1 = dt * dxdt( t, x, y, vx, vy ) ! ここからルンゲクッタ法の主要部分
dvx1 = dt * dvxdt( t, x, y, vx, vy ) ! 4元なので1番の増分が4つある(先週は2つだった)
dy1 = dt * dydt( t, x, y, vx, vy ) ! これらが同様に4番まで続く
dvy1 = dt * dvydt( t, x, y, vx, vy )
.....
x = x + (dx1 + 2*dx2 + 2*dx3 + dx4)/6. ! x座標を更新する.同様にあと3つ.
.....
初期条件は t=0.D0 で x=1.D0, y=0.D0, vx=0.D0, vy=1.D0とすること.またdt=1.D-2とすること.まずは700回ループを計算させる.
write(1,*) t, x, y
と,時刻,x座標,y座標と並べてファイルに出力する.gnuplotで以下のコマンドを実行することでアニメーションを観察すること.半径1の円運動をするはずである.
gnuplot> n=1
gnuplot> load 'anim.txt'
ここで,anim.txtの中身は以下のとおり.
set xrange [-1:1]
set yrange [-1:1]
if (n>700) exit
p "ファイル名" u 2:3 every 1:1:n:0:n:0 w p pt 7 ps 2, "sun.dat" w p pt 6 ps 3
pause 0.05
n=n+1
reread
"ファイル名"に結果を出力したファイル名を記入すること.時間ループの回数を"ループ回数"に記入すること.また,ファイル"sun.dat"は原点に存在する太陽の位置を表し,内容は
0.D0 0.D0
としておくこと.xrange, yrangeで指定されている値を変化させると,画面で表示される座標の範囲が変わる.適宜変更すること.
[2] ケプラーの法則
ケプラーの法則は、1619年にヨハネス・ケプラーによって解明された惑星の運動に関する法則である。ケプラーは、ティコ・ブラーエの観測記録から、太陽に対する火星の運動を推定し、以下のように定式化した。
- 第1法則 : 惑星は太陽をひとつの焦点とする楕円軌道上を動く。
- 第2法則 : 惑星と太陽とを結ぶ線分の描く面積は単位時間あたり常に一定である(面積速度一定)。
- 第3法則 : 惑星の公転周期の2乗は軌道の半長径の3乗に比例する。
[3] 第二法則を発見しよう
練習問題2
初速vy=0.5D0とする.軌道をアニメで観察すると楕円になっているはずである.nステップ目の座標とn+1ステップ目の座標,および原点(0,0)からなる三角形の面積を求めよ.この面積が時間とともにどう変化するかgnuplotを用いてグラフを作成せよ.x, yを増やす前に,xとyの値をxold, yold と別の変数に代入しておくと良い.
[4] 第三法則を発見しよう
練習問題3
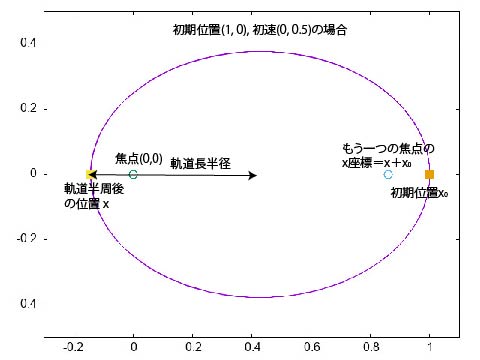
初速は0.5D0そのままで,惑星の初期x座標を3とおり変化させて計算を行う(1.D0, 1.5D0, 2.D0).惑星が太陽の周りを半周するのにかかる時間(周期の半分),および軌道長半径((初期x座標-軌道を半周したときのx座標)/2)を求めよ(位置関係は下図参照).横軸に周期(の半分),縦軸に軌道長半径をとりグラフを作成せよ.軌道長半径は周期の何乗に比例しているか? 軌道を半周したとき時間を求めるためには,前述したyoldをつかって,y*yold < 0.D0 となる時のx座標を求めればよい.
この条件が満たされた時にプログラムを停止させ,画面に座標および軌道長半径(および次の問題で使う,太陽以外のもう一つの焦点のx座標)を表示させるには以下のようにする.ここでx0は初期x座標.
if ( y * yold < 0.D0 ) then
write(*,*) t, (x0 - x)/2, x0 + x ! (x0-x)/2が軌道長半径,x0+xが焦点のx座標.
stop
endif
半周した時間,軌道長半径,もう一つの焦点の座標を左から並べたファイルを作成する.
0.14599999999999999 0.12844952574720644 0.24310094850558711
0.43300000000000000 0.26663349352131815 0.46673301295736369
1.3580000000000001 0.57141729378300232 0.85716541243399524
ケプラーの第3法則から,軌道長半径は周期の2/3 (=0.6666)乗に比例するはずである.上のデータファイルを以下のようにgnuplotでプロットすることで,第3法則を確かめること.set logで両対数グラフにする.
gnuplot> set log
gnuplot> p '上のファイル名', 0.465*x**(0.66666)
[5] 第一法則を発見しよう
練習問題4
練習問題3で用いた,初速=0.5D0, 初期x座標=1.D0で計算を行え.ケプラーの第一法則により軌道は楕円になっているはずである.
二つの点(焦点)からの距離の和が一定になる点の集合が楕円である.今の場合,一方の焦点は原点(0.D0, 0.D0),もう一方の焦点のy座標は0.D0, x座標は(初期x座標+軌道を半周したときのx座標)で与えられる(上図参照).この座標は練習問題3で求めているはずである.二つの焦点から惑星までの距離の和が一定になっていることを確かめよ.
[6] 宿題1 (1点:12/26日まで)
プログラムと,練習問題4の結果(距離の和の一定値)を送付すること.
[7] 宿題2 (1点:12/26日まで) 散乱角度:斥力の場合との比較
dt=1.D-2, 初期位置をx=20.D0, y=0.2D0,初期速度をvx=-5.D0, vy=0.D0とする.
この条件でシミュレーションすると,質点は右から原点に近づき,原点近くで引力により曲げられ,原点から遠ざかる.まったく同じシミュレーションを,力の符号をマイナスからプラスに変えて行えば,斥力が働く場合のシミュレーションとなる(同一電荷を持った粒子が接近する場合).これらふた通りのシミュレーションを行い,結果の軌道をgnuplotで観察すること.
set xrange [-20:20]
set yrange [-20:20]
if (n>700) exit
plot "引力のファイル" using 2:3 every 1:1:n:0:n:0 with points pt 7 ps 2,"sun.dat" with points pt 6 ps 3,"斥力のファイル" u 2:3 every 1:1:n:0:n:0 w p pt 7 ps 2
pause 0.01
n=n+1
reread
ファイル名はそれぞれ,時間t:x座標:y座標が記録されたファイル名に書き換えること.
次に,原点から遠ざかっていく速度と.x軸とがなす角度を引力と斥力の場合でそれぞれ求める.角度は,datan(vy/vx)で求めることができる(これで出る角度は度でなくラジアンなことに注意).
プログラムと,引力の場合と斥力の場合の角度を送付すること.
日程表へ戻る <<
|