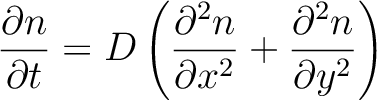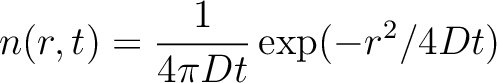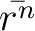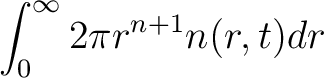数値解析法及び演習 第十一回

乱数とランダムウォーク
  1. 乱数の発生法
  2. ランダムウォーク
  3. 今日の宿題

[1]乱数の発生法

数値実験を行うと乱数が必要になる場合がある．コンピュータで乱数を発生させる方法はいくつかあって，そのうちの一つについて学ぶ．なお，この方法で発生できるのは「真の」乱数ではなく疑似乱数である．コンピュータでの乱数の発生法は非常に奥が深く，実用的にも重要．たとえばこの資料が参考になります．

混合合同法

これは，


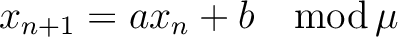\begin{displaymath} x_{n+1}=ax_n+b \quad {\rm mod}\,\mu \end{displaymath} (1)

によって順次乱数を発生させるものである．右辺で計算した値をμで割り，その余りを左辺に代入する．

練習問題1

3ビットの整数において乱数列を発生させ，その周期についてしらべてみよ． x1=1とし，μ=4とせよ．a=3,b=1, a=2,b=1, a=1,b=3の場合についてしらべよ．

32ビット整数（我々が使っているinteger）では，混合合同法をもちいると 

   program random
   implicit none
   integer :: i,j
   double precision :: ran
   
   do j = 1, 100
   
      i = 843314861 * i + 453816693

      if( i .lt. 0 ) i = ( I + 2147483647 ) + 1
      ran = dfloat(i) * 4.656612873D-10
   
      write(*,*) j,ran
    enddo
	
   end program random
をつかうことで[0,1)に規格化された乱数をつくることができる．ここでμ=2147483648（2の32乗）となっており，意図的に取り扱える整数の上限をオーバーさせることでmod(μ)の計算（割り算は時間がかかる）を回避している．また，4.656612873D-10は2147483648の逆数．

練習問題2

  1. 上のアルゴリズムを用いて乱数を10000回発生させ，平均値，分散を求めよ．真の値は平均値=1/2, 分散=1/12となる．

[2]ランダムウォーク

ブラウン運動と拡散

この動画は，牛乳に含まれる脂肪の粒子の運動を示しています．脂肪の粒子は周囲の水分子が絶え間なく衝突してくることで振動し，徐々に移動します．この運動はブラウン運動と呼ばれています．

気体や液体を構成する原子や分子においても同様の現象はおこり，拡散とよばれます．二次元平面を考えて，ある粒子の単位面積あたりの個数をnとすると，拡散は次の拡散方程式によって記述されます．


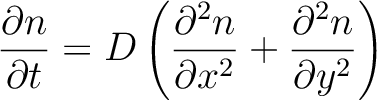\begin{displaymath} {\partial n\over \partial t}=D\left({\partial^2n\over \partial x^2} + {\partial^2n\over \partial y^2}\right) \end{displaymath} (2)

拡散方程式は偏微分方程式ですが，微分を無理矢理割り算で置き換えると


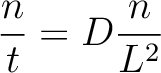\begin{displaymath} {n\over t}=4D{n\over L^2} \end{displaymath} (4)

と書くことができます．ここでLは球が存在している範囲の距離．これをtについて解くと


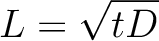\begin{displaymath} t={L^2\over 4D} \end{displaymath} (5)

となり，拡散した距離Lは時間の平方根に比例することがわかります．つまり，等速で運動するよりもはるかに遅い．

parameter文を利用したプログラムの作成

一辺が長さ1（整数）の正方形からできている碁盤の目を考える．原点(0,0)にn個の球が置いてある．乱数を発生させ，上下左右に存在する隣の格子点にそれぞれ確率1/4で移動する．n回乱数を発生させ，n個全ての球を一回移動させると１ステップが終了する．

このようなプロセスは「ランダムウォーク」（酔歩）と呼ばれます．分子の拡散，熱の伝導など地球科学においても非常に重要なプロセスを表現しています．

ランダムウォークのプログラムを作成しようとすると，球の数nの大きさの配列を複数用意する必要があります．たとえばi番目の球のx座標，y座標．100個の場合なら 

	integer :: x(100),y(100)
さらに，それぞれの球の原点からの距離も必要であれば dis(100)　などが追加されます． 配列のサイズを変化させる場合に複数箇所の数字を変化させる必要が発生し，書き間違いが起こります．このような場合はparamtere文が便利．parameter文は，ある文字列をその数字として読み替える，ということを指示します．つまりプログラム中でその文字列が登場すると，parameter文で定義された数値にコンパイル時におきかわります．parameter文で定義された変数は，プログラム中で別の値を代入はできません．

例： 
      integer, parameter :: n=1000
      integer :: x(n),y(n)

練習問題3

n個の球が上下左右にランダムウォークするプログラムを作成する．始めはすべて原点に球は存在する．確率 1/4 = 0.25D0 で上下左右に1（整数）だけ移動する．まずはn=10でプログラムを実行する．1000ステップ計算を実行すること．

プログラムのおおまかな構造 

  implicit none
  integer, parameter :: n = 10  ! 球の数
  integer :: x(n), y(n)  ! など他の変数も宣言する

  初期値の格納

  時間ステップのループ開始

  　　球に関するループ開始
  
       乱数を発生させ，球を移動させる

       write(1,*) x(i),  y(i)  !  アニメのための出力　練習問題５では消す
  
  　　球に関するループ終了

       write(1,*)     !   異なる時間ステップを区別するため空白行を入れる    
  
  時間ステップのループ終了


  プログラム終了

練習問題4

アニメーションを観察する．以下のテキストをanim.txtで保存する．ここでのkは時間ステップであることに注意． 
  set xrange [-100:100]
  set yrange [-100:100]

  if (k>1000) exit

  plot "ファイル名" every 1:1::k::k with points pt 7 ps 2

  pause 0.05

  k=k+1

  reread
gnuplot上で
gnuplot> k=1
gnuplot> load 'anim.txt'
とすることでアニメーションを観察すること．

練習問題5

前述したとおり，ランダムウォークはあっちにいったりこっちに行ったりするので，等速直線運動よりははるかにゆっくりと位置が変わります．そこで，粒子の平均移動距離がどう時間とともに増加するのかを調べます．

今日の宿題 (1点：1/10日まで)

練習問題５のプログラム，および時刻ー平均距離ー距離の標準偏差のデータファイルを送付すること．

[6] 追加の宿題 (1点：1/10日まで)

先ほどの問題において，平均値と標準偏差はほぼ平行であるものの平均値の方がいくぶん大きかった．この差がどこから来るのか考える．

拡散方程式（式２）のこの場合の解（t=0で原点に粒子が集中している場合）は

  $\displaystyle n(r,t)={1\over 4\pi Dt}\exp(-r^2/4Dt) $

とかける．ここで r=(x**2 + y**2 )**0.5である．D=1とすると，t=1, 2, 4の各時刻における粒子の分布はgnuplotにおいて上の式を使って 

plot exp(-x**2/4)/(4*pi),exp(-x**2/8)/(8*pi),exp(-x**2/16)/(16*pi)
とすると描くことができる．時間とともに分布が広がっていくことがわかる．

課題1: n(r,t)の式から，rの平均値とrの２乗の平均値をもとめ，(rの２乗の平均値-rの平均値の２乗)**0.5 から標準偏差を求めよ．rのn乗の平均値は以下の式で求めることができる．


$\displaystyle \bar{r^n}$ $\textstyle =$ $\displaystyle \int_0^\infty 2\pi r^{n+1} n(r,t) dr$ (7)

課題2: rの平均値 / rの標準偏差　はある定数となる．その定数をもとめ，本日の宿題として提出したファイルを使って（この例ではファイル名はfort.1） 

 plot 'fort.1','fort.1' u 1:($3*その定数）
とプロットすると二つの結果がほぼ重なるはずである．

課題２の定数を送付すること．


日程表へ戻る <<