[3] 台形公式
関数f(x)のある区間[x0, xn]の積分を考える.この区間をn個に分割すると積分は
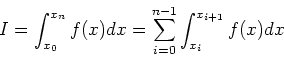 |
(3) |
| (4) |
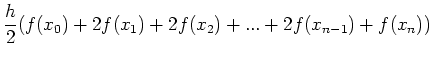 |
|||
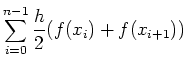 |
(5) |
練習問題2
| (6) |
計算機はミクロにはon,offの2状態しか扱うことができない. したがって計算機が計算している「数」は実際にはすべて2進数である. そこで計算機の内部で数がどう表されているか考えてみよう. ここではまず整数を考える.
簡単のために3ビットの計算機を考えよう. つまりこの計算機で取り扱えるのは3個の0, 1の組である. 3ビット計算機は次の表に表されるように整数を取り扱う.
| 符合のための1bit | 数値のための2bits | 表される整数 | 0 | 11 | 3 | 0 | 10 | 2 | 0 | 01 | 1 | 0 | 00 | 0 | 1 | 11 | -1(1に対する2の補数) | 1 | 10 | -2(2に対する2の補数) | 1 | 01 | -3(3に対する2の補数) | 1 | 00 | -4=2の(3-1)乗 |
|---|
補数,とは,元の数と補数を足した時に桁が上がる数のうち最小のものをいう.試しに,上の表をみて1(001)と1に対する2の補数(111)を足してみよ.111+001なので,桁が一つあがって1000となる.このような数を(2進数の場合)1に対する2の補数という.ちなみに1に対する1の補数というのもあって,この場合は桁上がりしない最大の数となり,001+110=111なので110となる.
この表から推測されるように, nビット計算機で取り扱える数は2の(n-1)乗-1からマイナス2の(n-1)乗までとなる. 次のプログラムを実行してみよ.
program max1
implicit none
integer :: n,m,k
n = 2147483647
m = n + 1
k = m + n + 1
write(*,*) n,m,k
end program max1
このプログラムはどうなるであろうか?
program max2
implicit none
integer :: n,m,k
n = 2147483648
m = n + 1
k = m + n + 1
write(*,*) n,m,k
end program max2
単精度実数は,実数を32個の0と1で表現する.
| 仮数部の符号1bit | 指数部の8bits | 仮数部(23bits) | 0 | 00000000 | 00000000000000000000000 |
|---|
| 仮数部の符号1bit | 指数部の11bits | 仮数部(52bits) | 0 | 00000000000 | 00000000000000000000000.. |
|---|
1bitはプラスかマイナスの符号につかう.8bitsを指数部に使う(倍精度の場合11bits).8個の0と1で-126から+127までの数を表す(倍精度の場合-1022から1023まで). ここからフォートランで用いることができる数値は2の127乗=10の38乗まで(倍精度の場合は2の10乗=10の308乗まで)ということになる.広く採用されているIEEE規格では基数を2ととることに注意.
残りの23個(倍精度の場合52個)を使って仮数部(0.234E5 だったら 0.234の部分)を表す.小数第1桁目は1ときまっているので表現はしないため実質2進数で24桁(倍精度の場合53桁)ということになる. 24桁なので仮数部で表せるもっとも小さな数は2の-24乗=0.6*10^(-7)(倍精度の場合0.1*10^(-15))となる.このことから数値的な誤差が発生する. 次のプログラムを実行させてみよう.
program small
implicit none
double precision :: a,b,c,d,e
a = 1.D-15
b = 1.D-16
c = 1.D0
d = c + a
e = c + b
write(*,"(3E26.18)") a,b,c,d,e
end program small
結果はどうなったであろうか? これが誤差を生み出す原因である.ここで見ら
れる誤差は二つあって
フォートランにはデフォルトでいくつかの関数が用意されているが,ユーザー が独自に関数を定義して用いたい場合は「関数副プログラム」というものをつかって関数 を定義することが出来る.使い方は
t function f(a1,a2,....aN) ...... f=..... return end
| function文 | f=.... | 関数副プログラムの定義をおこなう |
| t | 型宣言:double precision, integerなど |
|---|---|
| a1,a2,...aN | 仮引数:型宣言をすること |
b=f(c1,c2,....cn)のように引数を代入して行う.
たとえば, 1からnまでの総和を求める関数副プログラムは
integer function souwa(n)
implicit none
integer i,n
souwa = 0 ! ここで(n)はつかない
do i = 1, n
souwa = souwa + i ! ここでも(n)はつかない
enddo
end function
program sum
implicit none
integer souwa,n ! souwaを宣言する必要あり.(n)はつかない
read(*,*) n
write(*,*) souwa(n) ! ここではnを代入するので(n)がつく
end program sum
注意点
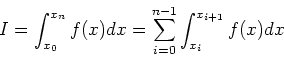 |
(3) |
| (4) |
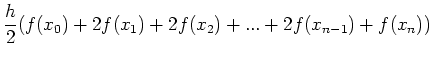 |
|||
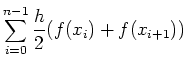 |
(5) |
| (6) |
| (8) |
| (9) |
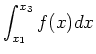 |
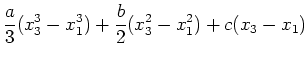 |
||
![$\displaystyle (x_3-x_1)\left[{a\over 3}(x_1^2+x_1x_3+x_3^2)+{b\over 2}(x_1+x_3)+c\right]$](img15.png) |
(10) |
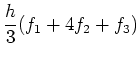 |
|||
![$\displaystyle 2h[{a\over 3}(x_1^2+x_1x_3+x_3^2)+{b\over 2}(x_1+x_3)+c]$](img18.png) |
(11) |
| (1) |
| (2) |
| (3) |
| (4) |