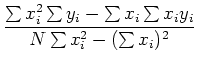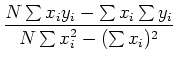FORTRANでは実数と整数を区別して変数に格納します. 正しい型の変数を用意しておかないと計算結果がおかしくなります. 変数の型には注意をはらうこと!
実数は必ず小数点がつく! 3.D0は実数,3は整数.
整数型と実数型の変数を混ぜて使うときには注意が必要である.以下に考えられるパ
ターンを挙げる.
- 整数型=整数型.L=M/N.演算結果は整数となる.小数点以下は切り捨てられる.
- 実数型=整数型.A=M/N.演算結果は整数となり,それが実数化されてAに代入される
.
- 整数型=実数型.M=B/C.演算の結果は実数であるが,左辺の整数型変数には小数点以
下が切り捨てられた整数が代入される.
- 実数型=実数型.A=B/C.演算の結果は実数.左辺にも実数が代入される.
- 整数型=整数と実数の混合演算.L=M/A.混合演算では整数が実数に変換された後演算
が行われる.その結果でた実数の値の小数点以下が切り捨てられて左辺に代入される.
- 実数型=整数と実数の混合演算.A=M/B.実数型=実数型と同じ.
implicit none
integer m, n, l
double precision a, b, c, d, s
real f, r
l=1/2
a=1/2
m=1.D0/2.D0
b=1.D0/2.D0
n=5/2.D0
c=5/2.D0
r = 16.1
s = 3.D0
s = s + r
write(*,'(3(I2,x),2(E24.16,x))') l, m, n, a, b
write(*,'(2(E24.16,x))') c, d
write(*,'(2(E24.16,x))') s, r
end
結果はどうなったであろうか? dの値は?
gnuplot(ニュープロットとよむ)は,UNIXシステムにおける簡便なグラフ描画
ソフトである.
起動は
gnuplot
で行われる.
最も基本的なデータは
-1.0 -3.2
0.0 -0.9
1.0 1.2
2.0 2.8
3.0 5.0
といった形で与えられる.左側のデータをx座標,右側のデータ(ファイル名を plot.datとする)をy座標とおもってxy平面上にプロットするときは,gnuplotを起動した画面で
plot 'plot.dat'
とするとグラフが描かれる.さらに
plot 'plot.dat' w l
とするとデータ点を線で結ぶ.また,gnuplotにはいろいろな関数が用意されていて,
plot sin(x)
とするとサインカーブを描いてくれる.三次元プロットも可能で
sp x**2 + y**2
とすると z=x**2 + y**2を描画する.
通常の変数(整数型,実数型ともに)は数値を一つしか格納できない.これでは多くのデータを扱うときに困る.そこで「配列」とよばれるものが用意されている.配列は複数の要素からなり,要素の番号を指定することで複数の数値を格納することができる.
配列名は英字で始まり,31文字以内の任意の英数字およびアンダースコア(_)からなる.大文字と小文字は区別されない.
配列の宣言:
宣言文 配列名(寸法の下限:寸法の上限)
例1
double precision a(10)
a(1)からa(10)まで要素を10個持つ倍精度実数型配列を宣言
例2
integer i(-1:8)
i(-1)からi(8)まで要素を10個もつ整数型配列を宣言
例:
implicit none
integer i
double precision a(10)
a(1)=1.D0
a(2)=2.D0
a(3)=3.D0
do i=1,10
write(*,*) i,a(i)
enddo
end
a(4)以降の要素はどう表示されたでしょうか?
練習問題1
次のプログラムを改造して,
- a(1)+a(2).... +a(10)
- a(1)**2+a(2)**2.... +a(10)**2
- a(1)*b(1)+a(2)*b(2)...+a(10)*b(10)
それぞれの総和を求めなさい.なお,以下のプログラムを基にすること.
implicit none
integer i
double precision a(10),b(10),sum(3)
do i=1,3
sum(i)=0.D0 ! 三つの和をそれぞれsum(1),sum(2),sum(3)に格納する.
enddo
do i=1,10
a(i)=1.D0*i ! a(i)には実数の1.D0, 2.D0,... 10.D0が格納される
b(i)=2.D0*i ! b(i)には実数の2.D0, 4.D0,... 20.D0が格納される
enddo
**ここに必要なプログラムを書き足して下さい**
end
練習問題2
上のプログラムを改造して,
- a(i), b(i)の平均値
- a(i), b(i)の分散
を求めなさい.
二つの量を測定したときに,そのあいだに線形の関係が期待されることがよくある.
もっともありそうな傾き(B)と切片(A)を求めるのが最小二乗法である.
最小二乗法では, 測定されたデータの組(x,y)にフィットする直線を求める. データxは正確に求められているとし, またデータyのバラツキは正規分布をしているものとする. この場合, フィットする直線をy=A+Bxとすると, A,Bはそれぞれ
となる. したがって切片Aと傾きBを算出するためには次の和をもとめればよい.
- Σx (xの総和)
- Σx*y (xかけるyの総和)
- Σx**2 (xの二乗の総和)
- Σy (yの総和)
練習問題3
plot.datを読み込ませ,最小二乗法によりフィットした
直線の傾きと切片を求めるプログラムを作成せよ. AとBを求めたら, その直線
とデータをgnuplotで描き, フィッテイングが正しいことを確かめよ.
データと直線を重ねてプロットするには
plot 'plot.dat', 2.2 + 3.4 * x
のように,コンマで続ける.2.2や3.4の場所には自分で求めたA, Bの値にすること.
練習問題3のプログラム, 答えを送ること. 〆切は10/27.
日程表へ戻る <<