数値解析法及び演習第十二回

[1]波動方程式

前回は，乱数を用いることで拡散方程式を解いた．今回は，同じく偏微分方程式である波動方程式を数値的に解く

x方向1次元の波動方程式は次式で与えられる．ここでu(x,t)は弦の変位や水面の高さに相当する．なお，cは波が伝わる速度である．

$\begin{displaymath} {\partial^2u(x,t)\over \partial t^2}=c^2{\partial^2u(x,t)\over \partial x^2} \end{displaymath}$

(1)

方程式の差分化

波動方程式をどうやって解くか？　まず，波が存在する空間を設定する．ここでは，長さLの空間を想定し，その空間上に等間隔 Δx で並んだ点を考える．その各点における u(x,t) を算出することを目標とする．各点に番号をつけ，i=0~N で表す．一方で時間も等間隔 Δt で進ませることにする．時間については1（t-Δt), 2(t), 3(t+Δt) で表すことにする．このように記号を決めてやると，u(i,3) を求めることが目標となる．

まず，u(x,t)のxに関する1階微分を考える．微分の定義通りに考えると

$\begin{displaymath} {\partial u\over \partial x}= {u(x+\Delta x,t)-u(x,t)\over \Delta x} + O(\Delta x) \end{displaymath}$

(2)

となるが，Δx が有限であるためにΔx のオーダーの誤差がつく．2階微分を同様に求めると

$\begin{displaymath} {\partial^2u\over \partial x^2} = {u(x+\Delta x,t) -2u(x,t) + u(x-\Delta x,t)\over \Delta x^2} + O(\Delta x^2) \end{displaymath}$

(3)

となる．先ほどの1階微分で生じていたΔxのオーダーの誤差はちょうど打ち消しあってΔxの２乗のオーダーに改善する．時間についての2階微分も同様なので結局波動方程式は

$\begin{displaymath} {u(x,t+\Delta t)-2u(x,t)+u(x,t-\Delta t)\over \Delta t^2} =c^2{u(x+\Delta x,t)-2u(x,t)+u(x-\Delta x,t)\over \Delta x^2} \end{displaymath}$

(4)

と近似できることがわかる．この変形を「方程式の差分化」と呼ぶ．この式を変形してやると

$\begin{displaymath} u(x,t+\Delta t)=c^2{\Delta t^2\over \Delta x^2} \left( u(... ...,t)-2u(x,t)+u(x-\Delta x,t) \right) +2u(x,t)-u(x,t-\Delta t) \end{displaymath}$

(5)

となる．ここで左辺の u(x, t+Δt）が未知数である．これがN個存在する．一方で右辺の量はすべて時刻t もしくは t-Δtにおける量であり，これはすべて既知である．注意：u(x, t+Δt）を求めるためには，u(x, t）だけでなくu(x, t-Δt）も必要である．これは時間に関して二階微分であるため．u(x, t+Δt）を書き換えると u(i, 3)となり，式を書き換えると以下のようになる．

$\begin{displaymath} u(i,k+1)=c^2{\Delta t^2\over \Delta x^2} \left( u(i+1,k)-2u(i,k)+u(i-1,k) \right) +2u(i,k)-u(i,k-1) \end{displaymath}$

(6)

式()において両端を考えてみる．i=0の場合，右辺に u(i-1,2)が存在しているため u(-1,2)となってしまいiの範囲から外れてしまう．したがってi=0, N では式（6）は適用できない．残りのN-2本の方程式しか存在しないことになってしまう．残りの2つの方程式はどこから持って来ればよいのだろうか？この式のことを「境界条件」と呼ぶ．境界条件には主に2種類あり，一つは境界における値を指定する場合（ディリクレ条件），もう一つは境界における傾きを指定する場合（ノイマン条件）である．たとえば計算領域の両端でu=0と固定したとするとディリクレ条件は

$\displaystyle u(0,k) = 0,\quad u(N,k) = 0$
$\displaystyle u(0,k-1) = 0,\quad u(N,k-1) = 0$			(7)

となる．一方で，両端でdu/dx=0とするとノイマン条件となり

$\displaystyle u(0,k) = u(1,k),\quad u(N,k) = u(N-1,k)$
$\displaystyle u(0,k-1) = u(1,k-1),\quad u(N,k-1) = u(N-1,k-1)$			(8)

となる．それぞれ式が2セットあるのは，時刻がt+Δtの値を求めるためには，時刻 t と t-Δtとの場合で二通りの数値が必要なためである．

一方で，時刻t=0において u(i,1)を指定してやらないと計算をはじめることができない．これを「初期条件」とよぶ．式（5）でわかる通り，時刻Δt後のuを求めるためには時刻tとt-Δtの二つの時間におけるuが必要である．ここから，まず始めのu(i,3)を求めるためにとu(i,1)とu(i,2)が必要ということになる．u(i,1)を与えたときに，u(i,2)をどう求めるか？ u(x, t+Δt)をテーラー展開すると

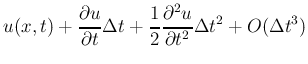$\displaystyle u(x,t+\Delta t)$	$\textstyle =$	$\displaystyle u(x,t)+{\partial u\over \partial t}\Delta t+{1\over 2}{\partial^2 u\over \partial t^2}\Delta t^2+O(\Delta t^3)$
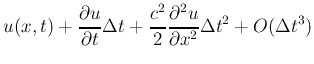	$\textstyle =$	$\displaystyle u(x,t)+{\partial u\over \partial t}\Delta t+{c^2\over 2}{\partial^2 u\over \partial x^2}\Delta t^2+O(\Delta t^3)$	(9)

となるので，u(i,2)は次式で求めることができることがわかる．

$\begin{displaymath} u(i,1) = u(i,0) + v(i,0)\Delta t + {c^2\Delta t^2\over 2\Delta x^2} \left( u(i+1,0) - 2u(i,0) + u(i-1,0) \right) \end{displaymath}$

(10)

ここで求めたu(i,2)と，初期条件 u(i,1)から，u(i,3)を求めることになる．

波動方程式を数値的に解く

練習問題1

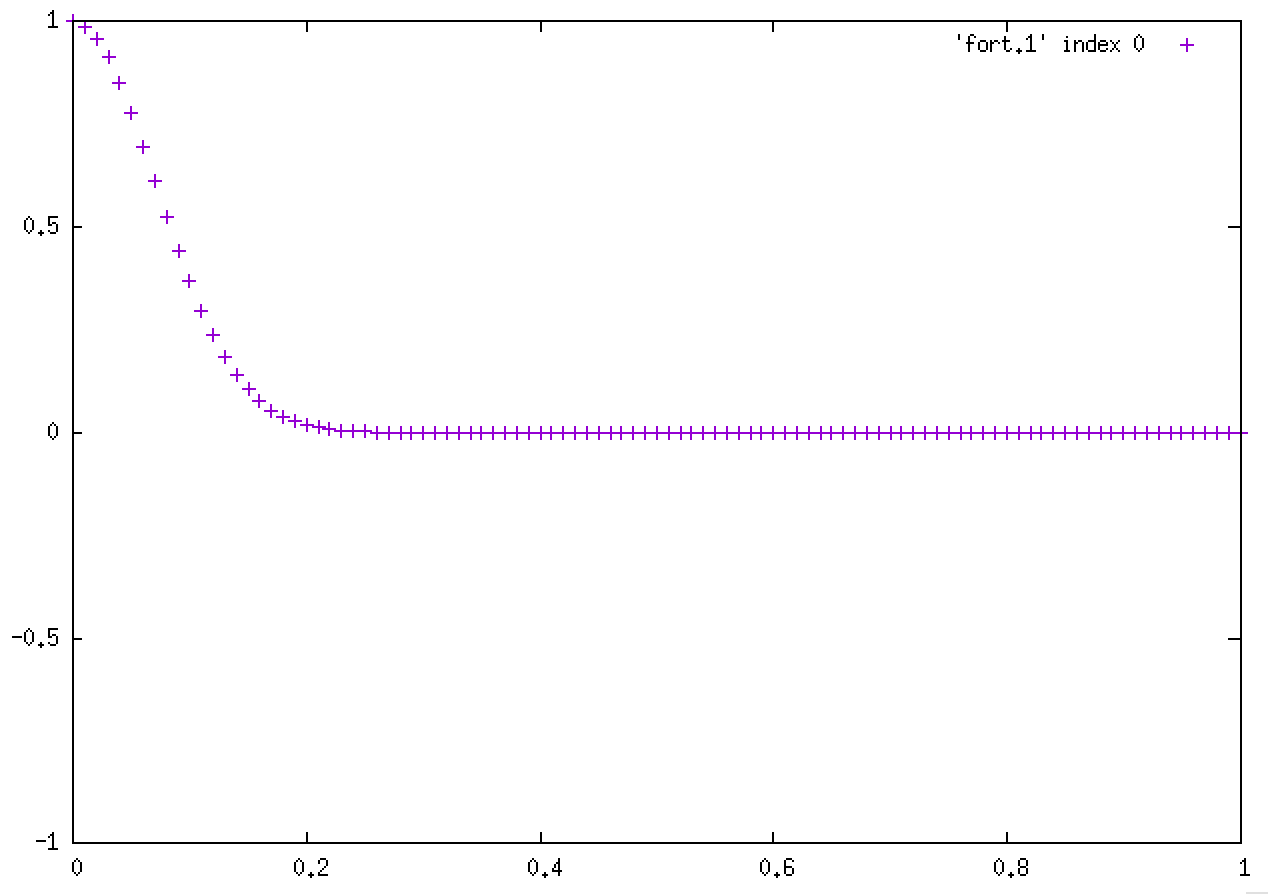
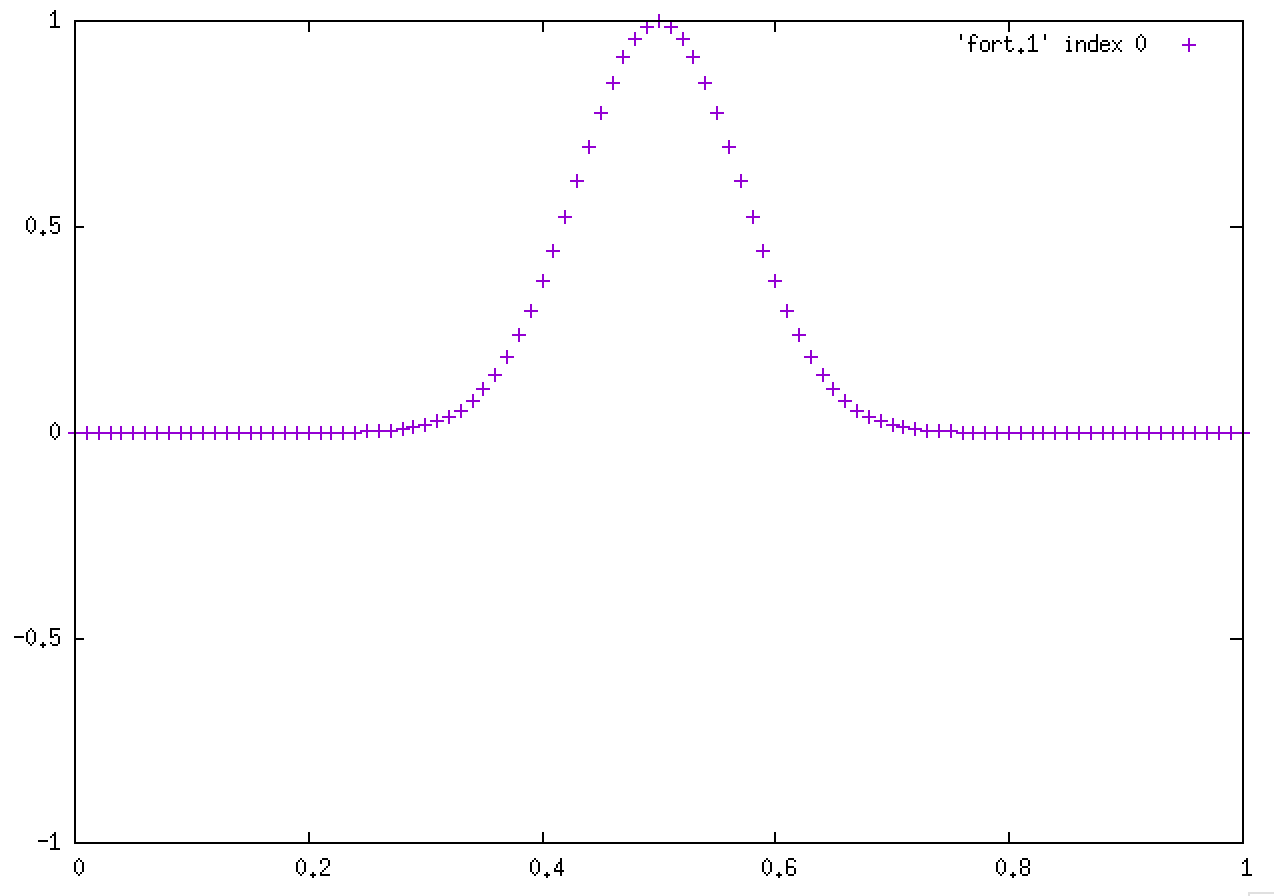
漸化式（式6）を条件（式7）もしくは（式8）で解くプログラムを作成せよ．L=1.D0, c=1.D0, N=100, Δx=0.01, Δt=0.01 とせよ．初期条件として

$\begin{displaymath} u(x,0) = \sin (\pi x/L) \end{displaymath}$

(11)

図1：式11のグラフ．

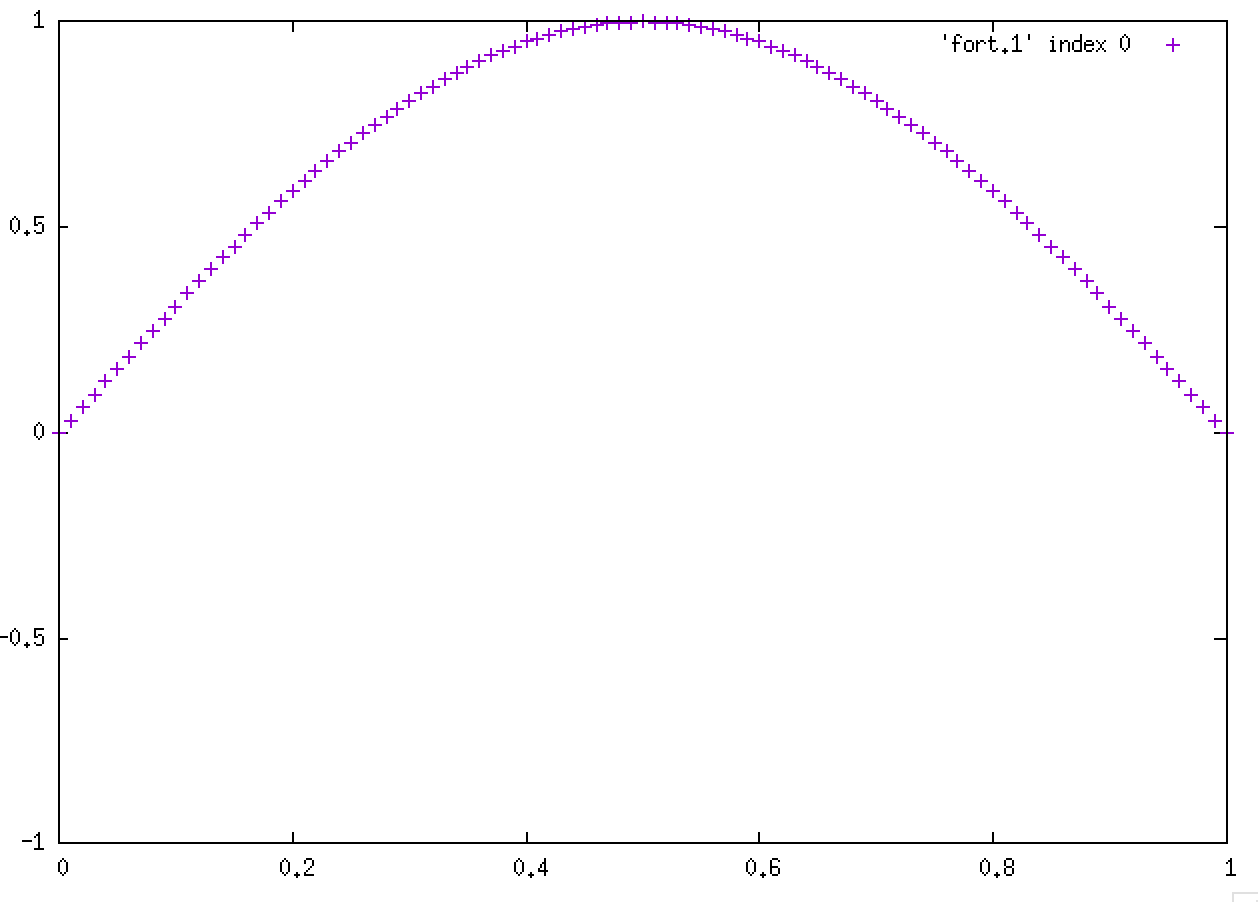
を与えること．初速度はゼロとする．この初期条件は上図で表されている．境界条件は固定端（式7）とすること．計算を実行する前に上図をよく見て，結果がどうなるか予想してノートに描いてみること．

結果は

  .....
  write(1,*) i*dx, u(x,2)
  enddo　<=  空間に関するループの終わり
  write(1,*)
  write(1,*)
  enddo  <=  時間に関するループの終わり

という形で出力すること．以下のテキストを anim.txt というファイル名で保存し，gnuplotで今までと同様に n=0 と load 'anim.txt' を実行すること．

set xrange [0:1]
set yrange [-1:1]

  if (n>3000) exit

  plot "fort.1" index n  w l

  pause 0.05

  n=n+1

  reread

練習問題2

練習問題1を，固定端でなく自由端（式8）で実行せよ．アニメを観察する前に，結果がどうなるかノートに図を描いて予想すること．

練習問題3

以下の初期条件を用い，固定端と自由端それぞれで計算を行え．初速度はゼロとする．固定端，自由端それぞれの場合について，結果がどうなるか予想してノートに描くこと．

$\begin{displaymath} u(x,0) = \exp\left(-(x-L/2)^2 \right) \end{displaymath}$

(12)

図2：式12のグラフ．

練習問題4

以下の初期条件で，固定端を用いて計算を行う．初速度はゼロとする．始めに，左から右に向かって波が進行する．波の頂点のx座標を算出し，横軸を時間，縦軸を頂点の座標でグラフを描く．頂点の座標が，c = 1　の速度で右に移動していることを確認せよ．

$\begin{displaymath} u(x,0) = \exp(-x^2) \end{displaymath}$

(13)

図3：式13のグラフ．

数値解析法及び演習第十二回

[1]波動方程式

方程式の差分化