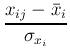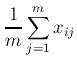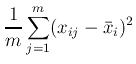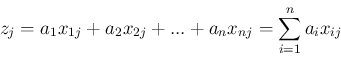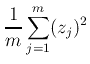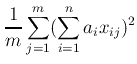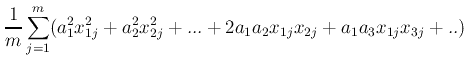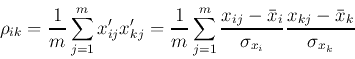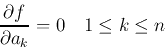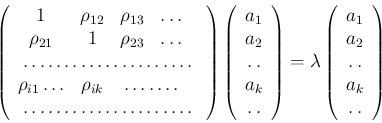数値解析法及び演習 第十三回

主成分分析
  1. 固有値，固有ベクトルを求めるサブルーチン
  2. 主成分分析
  3. 今日の宿題

[1] 固有値，固有ベクトルを求めるサブルーチン

n*nの対称行列a(n,n)および行列のサイズnを代入すると，固有値がd(n)に，規格化された固有ベクトルがv(n,n)に出力されるサブルーチン．v(i,j)がj番目の固有ベクトルのi成分，d(j)が対応する固有値となる．

注意点：代入する配列のサイズはn＊nになっていること．メインプログラムでは同じサイズの配列を宣言しておかないとエラーになる． 

SUBROUTINE jacobi(a,n,d,v)
  INTEGER n,np,nrot,NMAX
  DOUBLE PRECISION a(n,n),d(n),v(n,n)
  PARAMETER (NMAX=500)

  INTEGER i,ip,iq,j
  DOUBLE PRECISION c,g,h,s,sm,t,tau,theta,tresh,b(NMAX),z(NMAX)
  do ip=1,n
     do iq=1,n
        v(ip,iq)=0.D0
     enddo
     v(ip,ip)=1.D0
  enddo
  do  ip=1,n
     b(ip)=a(ip,ip)
     d(ip)=b(ip)
     z(ip)=0.D0
  enddo
  nrot=0
  do i=1,50
     sm=0.D0
     do ip=1,n-1
        do iq=ip+1,n
           sm=sm+abs(a(ip,iq))
        enddo
     enddo
     if(sm == 0.D0)return
     if(i .lt. 4)then
        tresh=0.2D0*sm/n**2
     else
        tresh=0.D0 
     endif
     do ip=1,n-1
        do iq=ip+1,n
           g=100.D0*dabs(a(ip,iq))
      
           if((i.gt.4).and.(dabs(d(ip))+g.eq.dabs(d(ip))) &
                .and.(dabs(d(iq))+g.eq.dabs(d(iq))))then
              a(ip,iq)=0.D0
           else if(dabs(a(ip,iq)).gt.tresh)then
              h=d(iq)-d(ip)
              if(dabs(h)+g.eq.dabs(h))then
                 t=a(ip,iq)/h 
              else
                 theta=0.5D0*h/a(ip,iq)
                 t=1./(dabs(theta)+dsqrt(1.+theta**2))
                 if(theta.lt.0.) t=-t
              endif
              c=1.D0/dsqrt(1+t**2)
              s=t*c
              tau=s/(1.+c)
              h=t*a(ip,iq)
              z(ip)=z(ip)-h
              z(iq)=z(iq)+h
              d(ip)=d(ip)-h
              d(iq)=d(iq)+h
              a(ip,iq)=0.
              do j=1,ip-1
                 g=a(j,ip)
                 h=a(j,iq)
                 a(j,ip)=g-s*(h+g*tau)
                 a(j,iq)=h+s*(g-h*tau)
              enddo
              do j=ip+1,iq-1
                 g=a(ip,j)
                 h=a(j,iq)
                 a(ip,j)=g-s*(h+g*tau)
                 a(j,iq)=h+s*(g-h*tau)
              enddo
              do j=iq+1,n
                 g=a(ip,j)
                 h=a(iq,j)
                 a(ip,j)=g-s*(h+g*tau)
                 a(iq,j)=h+s*(g-h*tau)
              enddo
              do j=1,n
                 g=v(j,ip)
                 h=v(j,iq)
                 v(j,ip)=g-s*(h+g*tau)
                 v(j,iq)=h+s*(g-h*tau)
              enddo
              nrot=nrot+1
           endif
        enddo
     enddo
     do ip=1,n
        b(ip)=b(ip)+z(ip)
        d(ip)=b(ip)
        z(ip)=0.
     enddo
  enddo

  return
END SUBROUTINE jacobi

練習問題1

以下の行列の固有方程式を手で解いて固有値，固有ベクトルを求めよ．さらに上に与えたサブルーチンjacobiを用いて以下の行列の固有値，固有ベクトルを求め，答えが一致することを確認せよ． 
  5.D0  2.D0
  2.D0  2.D0

[2] 主成分分析

記号の意味

先週と同じく，データの種類を i ，サンプル番号を j　で記す．データの種類は n ，サンプルは m　個あるものとする．データi，サンプル番号jの値をxijとする．

データの標準化

一般に異なる変量は異なる次元を持つ．そのためまず各変量をおなじように扱えるようにするために標準化という作業をおこなう．これは，平均値がゼロ，分散が1となるような変換をデータに施すことである．変量xijは


$\displaystyle x_{ij}'$ $\textstyle =$ $\displaystyle {x_{ij} - \bar{x}_i\over \sigma_{x_i}}$  
$\displaystyle \bar{x}_{i}$ $\textstyle =$ $\displaystyle {1\over m}\sum_{j=1}^mx_{ij}$  
$\displaystyle \sigma_{x_i}^2$ $\textstyle =$ $\displaystyle {1\over m}\sum_{j=1}^m (x_{ij}-\bar{x}_i)^2$ (1)

と変換される．標準化の結果, 全ての量の平均値が0, 分散が1となる. 以下，上につける ' を特別な場合を除いて省くことにする．

主成分

i番目のデータ種に着目したとする．xijのヒストグラムを作ったとすると，データは標準化されているので平均がゼロ，分散1の正規分布となる．これはiによらない．つまり，データを標準化すると全てのデータ種について同じ分布となっている．

複数のデータ種の線形結合を作り，この分布がどうなるか考える．全てのデータ種の平均値はゼロなので，線型結合の平均値もゼロ．しかし分散は一般に1とは異なってくる．分散が大きい場合と小さい場合とがありえる．分散が小さいということは，その線形結合に対する依存性が小さいということ．逆に分散が大きくなると，その組み合わせによってデータの依存性がよく説明できるということになる．

データの線型結合を


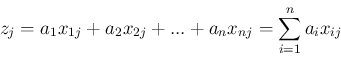\begin{displaymath} z_{j}=a_1x_{1j}+a_2x_{2j}+...+a_nx_{nj}=\sum_{i=1}^{n}a_ix_{ij} \end{displaymath} (2)

で与える．この線型結合の二乗和（平均値がゼロなので分散と同一）


$\displaystyle S$ $\textstyle =$ $\displaystyle {1\over m}\sum_{j=1}^m(z_{j})^2$  
  $\textstyle =$ $\displaystyle {1\over m}\sum_{j=1}^m(\sum_{i=1}^{n}a_ix_{ij})^2$  
  $\textstyle =$ $\displaystyle {1\over m}\sum_{j=1}^m(a_1^2x^2_{1j}+a_2^2x^2_{2j}+...+2a_1a_2x_{1j}x_{2j}+a_1a_3x_{1j}x_{3j}+..)$  
  $\textstyle =$ $\displaystyle a_1^2+a_2^2+...+2\rho_{12}a_1a_2+...$ (3)

ここでρikは相関係数となっていることに注意．


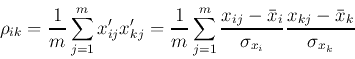\begin{displaymath} \rho_{ik} = {1\over m} \sum_{j=1}^mx'_{ij}x'_{kj} = {1\over... ...x}_i\over \sigma_{x_i}}{x_{kj} - \bar{x}_k\over \sigma_{x_k}} \end{displaymath} (4)

Sが「最大」になるaiの組み合わせを探す．ただし，aiベクトルの長さは1


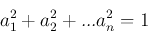\begin{displaymath} a_1^2+a_2^2+...a_n^2=1 \end{displaymath} (5)

という制約をつけておく必要がある（そうしておかないとaを大きくすればSが大きくなる）．このような条件では，ラグランジュの未定乗数法を用いることでaiを見つけることができる．ラグランジュの未定乗数λを用いて


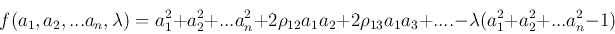\begin{displaymath} f(a_1,a_2,...a_n,\lambda) = a_1^2+a_2^2+...a_n^2+2\rho_{12}a_1a_2+2\rho_{13}a_1a_3+.... - \lambda(a_1^2+a_2^2+...a_n^2-1) \end{displaymath} (6)

という総和を作り，各aで偏微分すると


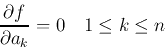\begin{displaymath} {\partial f\over \partial a_k}=0 \quad 1\le k \le n \end{displaymath} (7)


$\displaystyle 2a_1+2\rho_{12}a_2+2\rho_{13}a_3+.... - 2\lambda a_1$ $\textstyle =$ $\displaystyle 0$  
$\displaystyle 2\rho_{21}a_1+2a_2+2\rho_{23}a_3+.... - 2\lambda a_1$ $\textstyle =$ $\displaystyle 0$  
$\displaystyle .....$ $\textstyle =$ $\displaystyle 0$  
$\displaystyle 2\rho_{n1}a_1+2\rho_{n2}a_2 + .....2a_n - 2\lambda a_n$ $\textstyle =$ $\displaystyle 0$ (8)


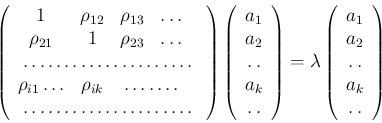\begin{displaymath} \left( \begin{array}{ccccc} 1 & \rho_{12} & \rho_{13} & \ld... ...ill}\\ a_k\\ \multicolumn{1}{c}{\dotfill} \end{array}\right) \end{displaymath} (9)

とまとめることができる．この行列を見ると，相関係数からなる「相関行列」の固有ベクトルが求めるaの組み合わせ，未定乗数λがその固有ベクトルの寄与ということになる．さらに，式（8）の第一行目の両辺にa1，2行目の両辺にa2，．．．第n行目にanを掛けて全て2で割ると


$\displaystyle a_1^2+\rho_{12}a_1a_2+\rho_{13}a_1a_3+....$ $\textstyle =$ $\displaystyle \lambda a_1^2$  
$\displaystyle \rho_{21}a_2a_1+a_2^2+\rho_{23}a_2a_3+....$ $\textstyle =$ $\displaystyle \lambda a_2^2$  
$\displaystyle .....$      
$\displaystyle \rho_{n1}a_na_1+\rho_{n2}a_na_2 + .....a_n^2$ $\textstyle =$ $\displaystyle \lambda a_n^2$ (10)

これらの式をすべて足し合わせると，式（3）と（5）から


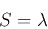\begin{displaymath} S = \lambda \end{displaymath} (11)

となることがわかる．よって，それぞれの主成分に対応して生じる分散は固有値となることがわかる．したがって固有値が大きければ大きいほどデータのばらつきの説明に寄与していることになる．一方で，全ての固有値の和は今の場合 n　であり，nが全ての固有ベクトルに対する分散の和となる．したがって，λ/n　が，その固有値の寄与率となる．

練習問題2

大きい順に2つの固有値と対応する固有ベクトルを求め，それぞれの主成分の寄与率を求めよ．また，それぞれの主成分に対応する固有ベクトルの値を観察することで，この集団の学力がどのような科目の組み合わせで特徴づけられているか議論せよ．なお，固有ベクトルは長さ1に規格化されていることに注意．

　
生徒番号 j 国語 x1 英語 x2 数学 x3 理科 x4
1 86 79 6768
2 71 75 7884
342 43 3944
4 62 58 9895
5 96 97 6163
6 39 33 4550
7 50 53 64 72
8 78 66 52 47
9 51 44 7672
10 89 92 9391

今日の宿題 (1/21日まで)

練習問題2のプログラムと結果を送付すること．




日程表へ戻る <<