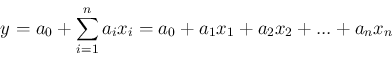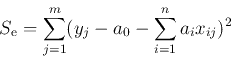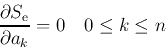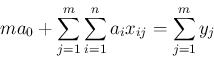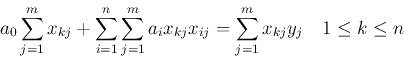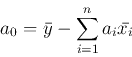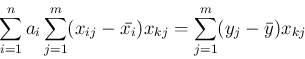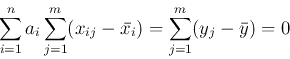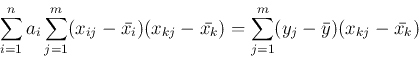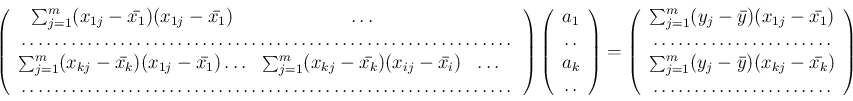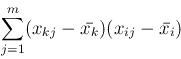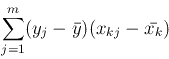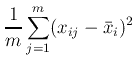数値解析法及び演習第十二回

[1] 逆行列を求めるサブルーチン

n*nの行列b(n,n)を代入すると，その逆行列がb(n,n）に上書きされて戻ってくるサブルーチン．

注意点：代入する配列のサイズはn＊nになっていること．メインプログラムでは同じサイズの配列を宣言しておかないとエラーになる．

      subroutine GJM(b,n)
      implicit none
      double precision b(n,n),max,W, a(n,2*n)
      integer Work(n),i,j,n,m,k,p,q,iw

       do i=1,n
          work(i)=i
       enddo

       do i = 1, n
          do j = 1, n
             a(i,j) = b(i,j)
          enddo
       enddo
       
       do i = 1, n
          do j = n+1,2*n
             if(i == j-n) then
                a(i, j) = 1.D0
             else
                a(i, j) = 0.D0
             endif
        enddo
      enddo


      
       do k=1,n
          max=abs(A(k,k))
          p=k
          q=k
          do j=k,n
             do  i=k,n
                if(max.lt.abs(A(i,j))) then
                   max=abs(A(i,j))
                   p=i
                   q=j
                endif
             enddo
          enddo
      
          do i=1,n
             W=A(i,k)
             A(i,k)=A(i,q)
             A(i,q)=W
          enddo
      
          do j=k,n+n
             W=A(k,j)
             A(k,j)=A(p,j)
             A(p,j)=W
          enddo
          i=Work(k)
          Work(k)=Work(q)
          Work(q)=i
          do j=k+1,n+n
             A(k,j)=A(k,j)/A(k,k)
          enddo
          do i=1,n
             if(i.ne.k) then
                do j=k+1,n+n
                   A(i,j)=A(i,j)-A(i,k)*A(k,j)
                enddo
             endif
          enddo
       enddo
      
      do j=n+1,n+n
         do i=1,n
            iw=Work(i)
            A(iw,n)=A(i,j)
         enddo
         do i=1,n
            A(i,j)=A(i,n)
         enddo
      enddo

       do i = 1, n
          do j = 1, n
             b(i,j) = a(i,j+n)
          enddo
       enddo
      
      return
      end

練習問題1

上に与えたサブルーチンGJM(b,n)を用いて以下の行列の逆行列を求めよ．もとの行列との積をとり，（ほぼ）単位行列になるかチェックせよ．

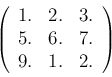$\begin{displaymath} \left( \begin{array}{ccc} 1. & 2. & 3.\\ 5. & 6. & 7.\\ 9. & 1. & 2. \end{array}\right) \end{displaymath}$

(1)

練習問題2

次の連立方程式をさきほどのサブルーチンを用いて解け.

$\displaystyle 5.x+2.y+6.z$	$\textstyle =$	$\displaystyle 7.$
$\displaystyle 2.x+2.8y+4.4z$	$\textstyle =$	$\displaystyle 7.8$	(2)
$\displaystyle 4.x+3.y+8.2z$	$\textstyle =$	$\displaystyle 6.$

練習問題3

プログラム中で単位行列を作成せよ．その逆行列を求めよ（答えは単位行列）．行列のサイズ(n)を100, 200, 400, 800と変化させ，行列のサイズとともに，計算時間がどう変化するか観察せよ．計算時間は

time ./a.out

とtimeコマンドを使用することで表示できる．横軸m, 縦軸計算時間（s)でグラフを書き，計算時間がmの何乗に依存しているか確認すること．

下の表はある駅徒歩圏内の中古マンションに関するデータである（多変量解析入門，永田・棟近共著，サイエンス社　より）．このデータに基づいて，価格を広さと築年数から予測できるか？　どの変数がより価格に影響を与えているか？　予測の精度はどのくらいか？　などを定量的に議論する手法を重回帰分析とよぶ．以下，サンプルの番号はj (1からmまで），データの種類の番号はi（1からnまで）とする．以下の式では，y_jがサンプル番号jのy，x_ijがデータ種類i，サンプル番号jのxとなる．この番号つけに注意してプログラムを式のとおりに作成すること．

サンプル番号j	広さ x₁ (m²)	築年数 x₂ (年)	価格 y (一千万円)
1	51	16	3.0
2	38	4	3.2
3	57	16	3.3
4	51	11	3.9
5	53	4	4.4
6	77	22	4.5
7	63	5	4.5
8	69	5	5.4
9	72	2	5.4
10	73	1	6.0

重回帰分析の目標は，n種類の変数x_iから量yを以下の重回帰モデルで予測することである．つまり，下の式でa_i (i=0からn）を決定することである．

$\begin{displaymath} y=a_0+\sum_{i=1}^{n}a_ix_i=a_0+a_1x_1+a_2x_2+...+a_nx_n \end{displaymath}$

(3)

最小二乗法と同様に，以下に示す計測値と予測値の差（残差平方和）S_eが最小になるように係数a_i を求める．

$\begin{displaymath} S_{\rm e}=\sum_{j=1}^m(y_j-a_0-\sum_{i=1}^{n}a_ix_{ij})^2 \end{displaymath}$

(4)

$\begin{displaymath} {\partial S_{\rm e}\over \partial a_k}=0 \quad 0\le k \le n \end{displaymath}$

(5)

上の偏微分から，a₀に対して

$\begin{displaymath} ma_0+\sum_{j=1}^{m}\sum_{i=1}^n a_ix_{ij}=\sum_{j=1}^m y_j \end{displaymath}$

(6)

a_i (i=1からn）に対して

$\begin{displaymath} a_0\sum_{j=1}^{m}x_{kj}+\sum_{i=1}^n \sum_{j=1}^{m}a_ix_{kj}x_{ij}=\sum_{j=1}^mx_{kj}y_j \quad 1\le k \le n \end{displaymath}$

(7)

と合計n+1本の式が導出される．式（6）をa₀について解くと

$\begin{displaymath} a_0=\bar{y}-\sum_{i=1}^n a_i\bar{x_{i}} \end{displaymath}$

(8)

となり，これを式(7)に代入すると

$\begin{displaymath} \sum_{i=1}^n a_i\sum_{j=1}^{m}(x_{ij}-\bar{x_i})x_{kj}=\sum_{j=1}^{m}(y_j-\bar{y})x_{kj} \end{displaymath}$

(9)

となる．

$\begin{displaymath} \sum_{i=1}^n a_i\sum_{j=1}^{m}(x_{ij}-\bar{x_i})=\sum_{j=1}^{m}(y_j-\bar{y})=0 \end{displaymath}$

(10)

に注意すると

$\begin{displaymath} \sum_{i=1}^n a_i\sum_{j=1}^{m}(x_{ij}-\bar{x_i})(x_{kj}-\bar{x_k}) =\sum_{j=1}^{m}(y_j-\bar{y})(x_{kj}-\bar{x_k}) \end{displaymath}$

(11)

と変形することができる．この式を行列で書き換えると

$\begin{displaymath} \left( \begin{array}{cccc} \sum_{j=1}^{m}(x_{1j}-\bar{x_1})(... ...-\bar{x_k})\\ \multicolumn{1}{c}{\dotfill} \end{array}\right) \end{displaymath}$

(12)

となる．ここから，左辺の行列の(k,i)要素は

$\begin{displaymath} \sum_{j=1}^{m}(x_{ij}-\bar{x_i})(x_{kj}-\bar{x_k})\quad {\rm for k, i} \end{displaymath}$

(13)

で与えらえ，右辺のベクトルのk要素は

$\begin{displaymath} \sum_{j=1}^m (y_j-\bar{y})(x_{kj}-\bar{x_k})\quad {\rm for k} \end{displaymath}$

(14)

となる．この要素で決まる連立方程式をとけばa_i (i=1からn）が求まり，その結果を式(8)に代入するとa₀を求めることができる．

練習問題4

はじめに示した表（マンション価格）について重回帰分析を行い，係数a₀，a₁，a₂を求めよ．

モデルの妥当性

値yの分散（のm倍）S_yyを変形すると

$\displaystyle S_{\rm yy} =\sum_{j=1}^m (y_j-\bar{y})^2$	$\textstyle =$	$\displaystyle \sum_{j=1}^m (y_j-(a_0+\sum_{i=1}^na_ix_{ij})+(a_0+\sum_{i=1}^na_ix_{ij})-\bar{y})^2$
	$\textstyle =$	$\displaystyle \sum_{j=1}^m(y_j-(a_0+\sum_{i=1}^na_ix_{ij}))^2 +\sum_{j=1}^m((a_0+\sum_{i=1}^na_ix_{ij})-\bar{y})^2$	(15)
$\displaystyle S_{\rm yy}$	$\textstyle =$	$\displaystyle S_{\rm e} + S_{\rm R}$
$\displaystyle S_{\rm R}$	$\textstyle =$	$\displaystyle \sum_{j=1}^m((a_0+\sum_{i=1}^na_ix_{ij})-\bar{y})^2$	(16)

となり，aを求めるために最小にした量S_e（予測値と実測値のずれ）と，予測値と平均値のずれS_Rの和であらわせることがわかる．S_RとS_yyの比を

$\begin{displaymath} R^2 \equiv {S_{\rm R}\over S_{\rm yy}} \end{displaymath}$

(17)

寄与率（決定係数）とよび，もともとのyの変動を，モデルによって説明できている割合を示す．

練習問題5

はじめに示した表（マンション価格）について寄与率を求めよ．

標準化

一般に異なる変量は異なる次元を持つ．そのためまず各変量をおなじように扱えるようにするために標準化という作業をおこなう．これは，平均値がゼロ，分散が1となるような変換をデータに施すことである．変量y_i，x_ijはそれぞれ

$\displaystyle y_j'$	$\textstyle =$	$\displaystyle {y_j - \bar{y}\over \sigma_y}$
$\displaystyle \sigma_y^2$	$\textstyle =$	$\displaystyle {1\over m}\sum_{j=1}^m (y_j-\bar{y})^2$
$\displaystyle x_{ij}'$	$\textstyle =$	$\displaystyle {x_{ij} - \bar{x}_i\over \sigma_{x_i}}$
$\displaystyle \sigma_{x_i}^2$	$\textstyle =$	$\displaystyle {1\over m}\sum_{j=1}^m (x_{ij}-\bar{x}_i)^2$	(18)