数値解析法及び演習第十三回

[1]乱数の発生法

数値実験を行うと乱数が必要になる場合がある．コンピュータで乱数を発生させる方法はいくつかあって，それについて学ぶ．なお，コンピュータで発生できるのは「真の」乱数ではなく疑似乱数である．

混合合同法

これは，

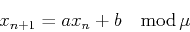$\begin{displaymath} x_{n+1}=ax_n+b \quad {\rm mod}\,\mu \end{displaymath}$

(1)

によって順次乱数を発生させるものである．右辺で計算した値をμで割り，その余りを左辺に代入する．

練習問題1

3ビットの計算機において乱数列を発生させ，その周期についてしらべてみよ． x₁=1とし，μ=4とせよ．a=3,b=1, a=2,b=1, a=1,b=3の場合についてしらべよ．

32ビット計算機では，混合合同法をもちいると

       I=843314861*I+453816693

      if(I.lt.0) I=(I+2147483647)+1
      ran=float(I)*4.656612873D-10

をつかうことで[0,1)に規格化された乱数をつくることができる．

練習問題2

解析的に平均値，標準偏差を求めよ．
乱数を10回発生させ，それぞれ画面に表示する．擬似乱数になっていることを確認せよ．
上のアルゴリズムを用いて乱数を発生させ，平均値，標準偏差を求めよ．乱数を発生させる回数を10, 100, 1000, 10000, 100000, 1000000と変化させてみよ．真の値にどう近づくか？

[2]ランダムウォーク

一辺が長さ１の正方形からできている格子を考える．原点(0,0)にn個の球が置いてある．乱数を発生させ，上下左右に存在する隣の格子点にそれぞれ確率1/4で移動する．n回乱数を発生させ，N個全ての球を一回移動させると１ステップが終了する．

parameter文の利用

このプログラムを作成すると，同じサイズ（球の数n)の配列を多数用意する必要がある．同じ数字を何回も書くのは面倒であり，さらに配列のサイズを変化させる場合に手間がかかる．そこでparamtere文を用いる．parameter文は，ある文字列をその数字として読み替える，ということを行う．つまりプログラム中でその文字列が登場すると，parameter文で定義された数値にコンパイル時におきかわる．注意点は，parameter文で定義された変数は，プログラム中で別の値を代入はできない．ということである．

例：

      integer n
      parameter (n=1000)
      double precision x(n),y(n)

fortran90以降においては以下のようにもかける．

      integer, parameter :: n = 1000
      double precision, dimension(n) :: x,y

練習問題3

n個の球がランダムウォークするプログラムを作成せよ．始めはすべて原点に球は存在する．確率1/4で上下左右に1.D0だけ移動する．まずはn=10でプログラムを実行する．10000ステップ計算を実行すること．

注意点

N個のx座標，y座標をファイルに書き出したら，その次には空白行を入れておくこと．

例：

   do i=1,n
     write(1,*) x(i),y(i)
   enddo
     write(1,*)

課題1

アニメーションを観察する．以下のテキストをanim.txtで保存する．

  set xrange [-100:100]
  set yrange [-100:100]

  if (n>1000) exit

  plot "ファイル名" every 1:1::n::n with points pt 7 ps 2

  pause 0.05

  n=n+1

  reread

gnuplot上で

gnuplot> n=1
gnuplot> load 'anim.txt'

課題2

球は原点からじょじょに遠ざかる．つまり，「拡散」する．格子上ではなくて連続空間を考えると，単位面積あたりに存在する球の数nは，次の拡散方程式に従って変化する．

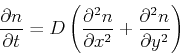$\begin{displaymath} {\partial n\over \partial t}=D\left({\partial^2n\over \partial x^2} + {\partial^2n\over \partial y^2}\right) \end{displaymath}$

(2)

ここでDは拡散係数と呼ばれる量であり，一回の移動量Δxを１，時間ステップΔtの長さを１とすると次式で与えられる．

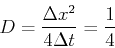$\begin{displaymath} D={\Delta x^2\over 4\Delta t}={1\over 4} \end{displaymath}$

(3)

拡散方程式は偏微分方程式であるが，微分を無理矢理割り算で置き換えると

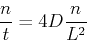$\begin{displaymath} {n\over t}=4D{n\over L^2} \end{displaymath}$

(4)

と書くことができる．ここでLは球が存在している範囲の距離である．これをtについて解くと

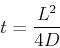$\begin{displaymath} t={L^2\over 4D} \end{displaymath}$

(5)

となり，距離Lだけ拡散するにはL**2/4Dだけ時間がかかるということが分かる． N個の球それぞれについて原点からの距離を計算する．この距離が初めて5, 10, 15, 20よりも大きくなった時刻を記録する．つまり球一つにつき４種類の時刻を記録する．この４種類の時刻のN個の平均値を算出し，横軸距離，縦軸時刻でグラフを書く．t=x**2が成立していることを確かめよ．N=1000個とする．

課題3

中心から距離が5よりも内側に存在している球の数を考える．球は外側に拡散してゆくので，この数は時間と共に小さくなる．

(5)式を参考に，この数が時刻tの何乗に比例して小さくなるか解析的に求めよ．
課題のプログラムを修正し，時刻とこの数をファイルに書き出す．gnuplotで両対数グラフを作成し，上で解析的に求めた時刻依存性を確認せよ．

何乗に比例するか，その数と修正したプログラムを送付すること．

数値解析法及び演習 第十三回