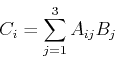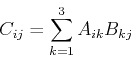数値解析法及び演習 第五回

行列の掛け算
  1. 今日の目標
  2. 配列へ初期値の代入
  3. 行列の掛け算
  4. 今日の宿題

[1] 今日の目標

  1. 初期値の代入
  2. 行列の掛け算を行なう

[2] 配列へ初期値の代入

配列に初期値を代入しておくには，data文を用いるやりかたと，配列式を用いるやりかたがある．すべての要素に同じ値を代入するときは，配列式が便利である．部分的に異なる値を代入しておく場合は，data文を用いる．

[2.1]DATA文

配列，変数を宣言した後に記述する．構文は以下のとおり．

data 変数や配列などの並び / 定数の並び /

例： 
  implicit none
  integer i,j
  double precision a(3,3),b
  data a,b / 4*0.D0, 5*1.D0, 10.D0 /

  do i=1,3
     write(*,*) (a(i,j),j=1,3)
  enddo
    write(*,*) b

  end

4*0.D0と書くと，始めの４つの要素にゼロを代入する．引き続いて5*1.D0で残りの５つの要素に1.D0が代入される．上の例で，どの要素に0.D0が，どの要素に1.D0が格納されているか注意すること．また，変数や配列の要素の数と，定数の数が異なるとエラーになるので注意すること．

[2.2]配列式

配列を用いて式を記述することができる．要素の数が同じであれば，加減乗除が可能．しかし，各要素についての演算を行うだけなので，次節で取り扱う通常の意味での行列の積にはなっていないので注意．

例： 
  implicit none
  integer i,j
  double precision a(3,3),b(3,3),c(3,3)

    a=1.D0
    b=2.D0

   c=a+b

    do i=1,3
      write(*,*) (c(i,j),j=1,3)
    enddo

    write(*,*)

   c=a*b

    do i=1,3
      write(*,*) (c(i,j),j=1,3)
    enddo

    write(*,*)

   c=a/b

    do i=1,3
      write(*,*) (c(i,j),j=1,3)
    enddo

   end

上の例では，配列a,bの全ての要素に1.D0と2.D0がそれぞれ代入され，配列の要素ごとに足し算，掛け算，割り算が行われる．通常の意味での行列の積や逆行列との積とはまったく異なるので注意すること．

[3] 行列の掛け算

[3.1]行列を取り扱う際のポイント

例：行列とベクトルの積

例えば，3×3の行列Aと，3次元ベクトルBの積を考える．この積はベクトルであり，それをCとする．数式で書くと以下になる．


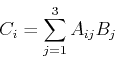\begin{displaymath} C_i=\sum_{j=1}^{3} A_{ij}B_j \end{displaymath} (1)

式通りにプログラムを書くと次になる． 

  do j = 1,3
  
     C(i) = C(i) + A(i,j) * B(j)

  end do

[3.2]行列の掛け算

先ほどの例と同様に，行列AとBとの積を考える．この結果は行列となり，それをCとすると次の式になる．この式を参考に行列の掛け算を行う．


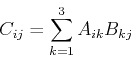\begin{displaymath} C_{ij}=\sum_{k=1}^{3} A_{ik}B_{kj} \end{displaymath} (2)

hai1.dat 
2.D0 3.D0 4.D0         
5.D0 6.D0 7.D0        
8.D0 9.D0 10.D0
hai2.dat 
1.D0 2.D0 3.D0 
4.D0 5.D0 6.D0
2.D0 4.D0 6.D0
上の二つの3行3列の行列をそれぞれ hai1.dat，hai2.dat とする．

練習問題

  1. ファイルから数値を読み込み，それぞれ配列a(3,3),b(3,3)に値を格納しなさい．
  2. それぞれの行列の対角和を求めなさい．
  3. この行列の掛け算を行い，結果を画面に出力するプログラムをつくりなさい.
  4. 配列aに格納された行列（hai1.dat)を10乗して結果を画面に出力するプログラムをつくりなさい.

[4] 今日の宿題

練習問題のプログラム, 答えを送ること. 〆切は11/7.


日程表へ戻る <<