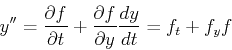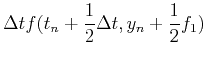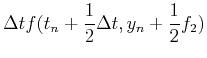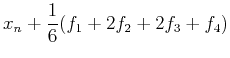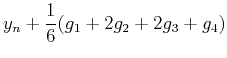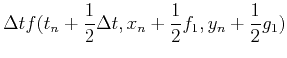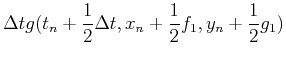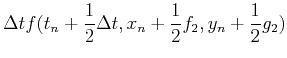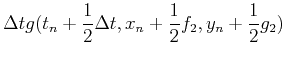数値解析法及び演習 第九回

常微分方程式
  1. 関数副プログラム
  2. Δtの二次の精度
  3. ルンゲクッタ法
  4. 連立1階微分方程式
  5. gnuplotでアニメ
  6. 今日の宿題

[1] 関数副プログラム

フォートランにはデフォルトでいくつかの関数が用意されているが，ユーザー が独自に関数を定義して用いたい場合は「関数副プログラム」というものをつかって関数を定義することが出来る．使い方は


t function f(a1,a2,....aN)
......
f=.....
return
end
function文 f=.... 関数副プログラムの定義をおこなう
t 型宣言：real*8, integerなど
a1,a2,...aN 仮引数：型宣言をすること
プログラム中で用いる時は, 

b=f(c1,c2,....cn)
のように引数を代入して行う．

たとえば, 1からnまでの総和を求める関数副プログラムは 

      integer function souwa(n)
      implicit none
      integer i,n

      souwa=0
      do i=1,n
      souwa=souwa+i
      enddo
      return
      end

      implicit none
      integer souwa,n
      read(5,*) n
      write(6,*) souwa(n)
      end

注意点

練習問題1

n!を計算する関数副プログラム fact(n)を作成せよ．

[2]常微分方程式その2 「Δtの二次の精度」

オイラー法における誤差はΔtに比例する(一ステップの誤差はΔtの二乗に比例するため：これはなぜか？)．すなわち誤差を10分の1にしたければΔtを1/10にする必要がある．これは計算にかかる時間が10倍になることを意味する．これでは時間がかかってしょうがない．そこでΔtの2乗，4乗に誤差が比例するようなアルゴリズムが存在する．4乗に比例するものはルンゲクッタ法と呼ばれ広く用いられている．

ルンゲクッタ法に入る前に誤差がΔtの2乗に比例するアルゴリズムについて考えてみよう．


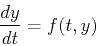\begin{displaymath} {dy\over dt}=f(t,y) \end{displaymath} (1)


という微分方程式が与えられたものとする．タイムステップがΔtのとき，n+1ステップ目のyの値yn+1は，ynを用いて

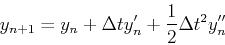\begin{displaymath} y_{n+1}=y_n+\Delta t y_n'+{1\over 2}\Delta t^2 y_n'' \end{displaymath} (2)

と書くことができる．ここでy''は二次の微係数で


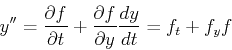\begin{displaymath} y''={\partial f\over \partial t}+{\partial f\over \partial y}{dy\over dt} =f_t+f_yf \end{displaymath} (3)

となる．2項出てくることに注意．これを用いると先ほどの式は


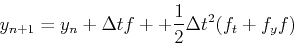\begin{displaymath} y_{n+1}=y_n+\Delta t f++{1\over 2}\Delta t^2 (f_t+f_yf) \end{displaymath} (4)

のようにかきかえられる．ここでポイントは，我々はft,fyを知らないと言うことである．なので別の式でさらに書き替えないといけない．そのため式(8)が，以下のように書けるものと仮定する．


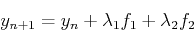\begin{displaymath} y_{n+1}=y_n+\lambda_1f_1+\lambda_2f_2 \end{displaymath} (5)

ここでf1，f2は


$\displaystyle f_1$ $\textstyle =$ $\displaystyle \Delta t f(t_n,y_n)$ (6)
$\displaystyle f_2$ $\textstyle =$ $\displaystyle \Delta t f(t_n+\alpha\Delta t,y_n+\beta f_1)$ (7)

である．f2の中身に注意．f1，f2はそれぞれtnでの傾き，および傾きk1でΔt秒進んだとしたときのt+Δt秒後の傾きを表す．この二つの傾きを適当に重ね合わせることによりΔtの二乗の精度にすることができる．(11)式をテーラー展開すると，λ1，λ2，α，βの間の関係式が


$\displaystyle \lambda_1+\lambda_2$ $\textstyle =$ $\displaystyle 1$ (8)
$\displaystyle \lambda_1\alpha$ $\textstyle =$ $\displaystyle {1\over 2}$ (9)
$\displaystyle \lambda_2\beta$ $\textstyle =$ $\displaystyle {1\over 2}$ (10)

と求めることができる．求めるべき数が4つあるのに式が３つしか存在しない．なのでいろいろな値の組み合わせが


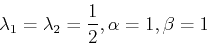\begin{displaymath} \lambda_1=\lambda_2={1\over 2}, \alpha=1, \beta=1 \end{displaymath} (11)


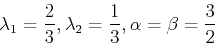\begin{displaymath} \lambda_1={2\over 3}, \lambda_2={1\over 3}, \alpha=\beta={3\over 2} \end{displaymath} (12)

といったようにありうる．いずれの場合も二次の精度まで正しく計算できる．つまり一ステップの誤差はΔtの3乗に比例する. 今回は(11)式を採用し，以下の(13)-(15)式で積分を行う．


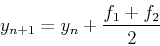\begin{displaymath} y_{n+1}=y_n+{f_1+f_2\over 2} \end{displaymath} (13)


$\displaystyle f_1$ $\textstyle =$ $\displaystyle \Delta t f(t_n,y_n)$ (14)
$\displaystyle f_2$ $\textstyle =$ $\displaystyle \Delta t f(t_n+\Delta t,y_n+f_1)$ (15)

練習問題2

式(13),(14),(15)を用いて先週の宿題を解け．オイラー法の場合と精度を比較せよ．

[3] ルンゲクッタ法

先ほどのアルゴリズムの誤差はΔtの二乗である．これを4乗に高めたのがルンゲクッタ法である．

さきほどと同じ考え方を使うと，ルンゲクッタ法のアルゴリズムは以下のようになる．


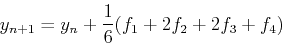\begin{displaymath} y_{n+1}=y_n+{1\over 6}({f_1+2f_2+2f_3+f_4}) \end{displaymath} (16)


$\displaystyle f_1$ $\textstyle =$ $\displaystyle \Delta t f(t_n,y_n)$  
$\displaystyle f_2$ $\textstyle =$ $\displaystyle \Delta t f(t_n+{1\over 2}\Delta t,y_n+{1\over 2}f_1)$  
$\displaystyle f_3$ $\textstyle =$ $\displaystyle \Delta t f(t_n+{1\over 2}\Delta t,y_n+{1\over 2}f_2)$  
$\displaystyle f_4$ $\textstyle =$ $\displaystyle \Delta t f(t_n+\Delta t,y_n+f_3)$ (17)

練習問題3

式(16),(17)を用いて，ルンゲクッタ法を用いて先の例の積分を行え．３つの場合の誤差を比較せよ．

[4] 連立微分方程式

先ほどのルンゲクッタ法は多変数に拡張できる．例えば，x=x(t)とy=y(t)がそれぞれ


$\displaystyle {dy\over dt}$ $\textstyle =$ $\displaystyle f(t,y,z)$  
$\displaystyle {dz\over dt}$ $\textstyle =$ $\displaystyle g(t,y,z)$ (18)

にしたがって進化する場合は，以下のようにアルゴリズムを組めばよい．


$\displaystyle y_{n+1}$ $\textstyle =$ $\displaystyle y_n+{1\over 6}(f_1+2f_2+2f_3+f_4)$  
$\displaystyle z_{n+1}$ $\textstyle =$ $\displaystyle z_n+{1\over 6}(g_1+2g_2+2g_3+g_4)$ (19)


$\displaystyle f_1$ $\textstyle =$ $\displaystyle \Delta t f(t_n,y_n,z_n)$  
$\displaystyle g_1$ $\textstyle =$ $\displaystyle \Delta t g(t_n,y_n,z_n)$ (20)


$\displaystyle f_2$ $\textstyle =$ $\displaystyle \Delta t f(t_n+{1\over 2}\Delta t,y_n +{1\over 2}f_1,z_n+{1\over 2}g_1)$  
$\displaystyle g_2$ $\textstyle =$ $\displaystyle \Delta t g(t_n+{1\over 2}\Delta t,y_n +{1\over 2}f_1,z_n+{1\over 2}g_1)$ (21)


$\displaystyle f_3$ $\textstyle =$ $\displaystyle \Delta t f(t_n+{1\over 2}\Delta t,y_n +{1\over 2}f_2,z_n+{1\over 2}g_2)$  
$\displaystyle g_3$ $\textstyle =$ $\displaystyle \Delta t g(t_n+{1\over 2}\Delta t,y_n +{1\over 2}f_2,z_n+{1\over 2}g_2)$ (22)


$\displaystyle f_4$ $\textstyle =$ $\displaystyle \Delta t f(t_n+\Delta t,y_n+f_3,z_n+g_3)$  
$\displaystyle g_4$ $\textstyle =$ $\displaystyle \Delta t g(t_n+\Delta t,y_n+f_3,z_n+g_3)$ (23)

練習問題5

質点の投げ上げの数値シミュレーションを行う．今回解く方程式は以下の連立微分方程式となる．


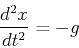\begin{displaymath} {d^2x\over dt^2}=-g \end{displaymath} (24)


$\displaystyle {dx\over dt}$ $\textstyle =$ $\displaystyle y$  
$\displaystyle {dy\over dt}$ $\textstyle =$ $\displaystyle -g$ (25)

式(25)で与えられる連立微分方程式を解け．g=1，t=0でx=0.D0, y=1.D0　とすること．Δt=1.D-2でt=2となるまで積分せよ．

[5] gnuplotでアニメ

gnuplotを用いて簡単なアニメーションを作ることができる．先ほどの練習問題5の結果を可視化しよう．連立微分方程式を解いた結果を，時間，0.,　x（座標）　y（速度）と4つの数値を並べてファイルに書き出す．さらに，以下の内容でanim.txtというファイルを作成する．

CCCCCCCCCCCC この下からanim.txt CCCCCCCCCCCCCCCCCCC 
  set xrange [-1:1]
  set yrange [0:1]

  if (n>200) exit

  plot "ファイル名" using 2:3 every 1:1:n:0:n:0 with points pt 7 ps 2

  pause 0.05

  n=n+1

  reread
CCCCCCCCCCCC この上までanim.txt CCCCCCCCCCCCCCCCCCC

gnuplotを起動し，以下のコマンドによってアニメーションを見ることができる．

gnuplot> n=1
gnuplot> load 'anim.txt'

アニメが観察できたら，初速(y)を変化させて行ってみる．t=0で y=1.45 としたらどうなるだろうか？

[6] 今日の宿題 (1/14日まで)

練習問題５




日程表へ戻る <<