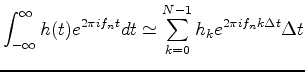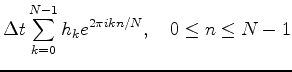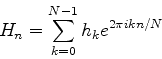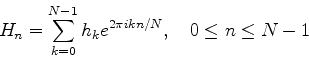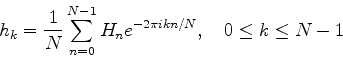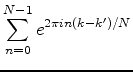数値解析法及び演習第十二回

[1] フーリエ変換の復習

フーリエ変換はさまざまな場面で出会うことになる. 地震の波形解析, 気候変動の解析, 地層の縞の解析などが典型的な例である. 今週と来週は離散データをフーリエ変換する手法を学ぶ. 今週は離散フーリエ変換のアルゴリズムを作成し, 来週はそれを用いる際の注意点および応用を学ぶ.

時間の関数h(t)が与えられたとしよう. h(t)のフーリエ変換, その逆変換は次式で与えられる. （注：一般には2πfではなくてωが用いられるが, ここでは計算の便利のため2πfを使う）

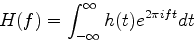$\begin{displaymath} H(f)=\int^{\infty}_{-\infty}h(t)e^{2\pi ift}dt \end{displaymath}$

(1)

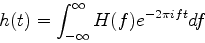$\begin{displaymath} h(t)=\int^{\infty}_{-\infty}H(f)e^{-2\pi ift}df \end{displaymath}$

(2)

フーリエ変換を行うと関数h(t)は関数H(f)に変換される. H(f)は一般に複素数となる. その絶対値の二乗は, 周波数f～f+dfに含まれるパワーになる. したがって, フーリエ変換すると, どの周波数成分が卓越しているかが分かる事になる. また，h(t)が実数の場合はH(-f)=H(f)^*(H(f)の複素共役）となることに注意．

以下でフーリエ変換を議論するときは, 次の形式でデルタ関数を書いておくと都合がよい.

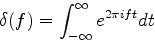$\begin{displaymath} \delta (f)=\int_{-\infty}^{\infty}e^{2\pi i ft}dt \end{displaymath}$

(3)

[2]離散フーリエ変換

我々が得るデータは普通離散データである. この場合, 一定の時間間隔Δtで物理量が計測される. 次の時刻t_nについてN個のデータが得られているとしよう.

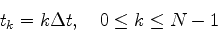$\begin{displaymath} t_n={n\Delta t},\quad 0\le n\le N-1 \end{displaymath}$

(4)

Δtについて, ナイキストの臨界周波数という次式で定義される周波数が存在する.

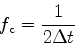$\begin{displaymath} f_{\rm c}={1\over 2\Delta t} \end{displaymath}$

(5)

ナイキストの臨界周波数がなぜ重要かというと, この周波数以上の成分は正しくフーリエ変換されないためである. このため, 離散フーリエ変換をする時の周波数の上限が決まる.

ナイキストの臨界周波数の存在から, 離散フーリエ変換を行った場合に我々が得ることのできるフーリエ変換成分は-fcからfcまでであることが分かった. データがN個あるものとすると, このデータから得られるフーリエ変換成分もたかだかN個しかない. そこで次の周波数についてフーリエ変換を求めることにしよう.

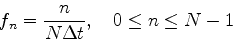$\begin{displaymath} f_n={n\over N\Delta t},\quad 0\le n\le N-1 \end{displaymath}$

(6)

式（1）を和で置き換えると以下のようになる.

$\displaystyle H(f_n)$	$\textstyle =$	$\displaystyle \int^{\infty}_{-\infty}h(t)e^{2\pi if_nt}dt\simeq \sum_{k=0}^{N-1}h_ke^{2\pi if_nk\Delta t}\Delta t$
	$\textstyle =$	$\displaystyle \Delta t\sum_{k=0}^{N-1}h_ke^{2\pi i kn/N}, \quad 0\le n\le N-1$	(7)

一般に離散フーリエ変換は上式からΔtをとった

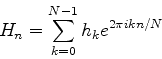$\begin{displaymath} H_n=\sum_{k=0}^{N-1}h_ke^{2\pi i kn/N} \end{displaymath}$

(8)

を指す．このように定義しておくと次元によらずまた逆変換との対応もよく見える．

練習問題1

H_-n=H_N-nが成立している事を確認せよ. ここから，Hは周期Nの周期関数であることになる．

上の問題から, H_-n=H_N-nであることが分かる. 0からN/2までは周波数0からfcまで対応し, N/2からN-1までは周波数-fcから-1/NΔtまでが対応することになる. すると最終的に求めるべき離散フーリエ変換は次式となる.

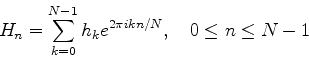$\begin{displaymath} H_n=\sum_{k=0}^{N-1}h_ke^{2\pi i kn/N}, \quad 0\le n\le N-1 \end{displaymath}$

(9)

n番めの周波数成分のパワーは，実部の二乗と虚部の二乗の和

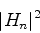$\begin{displaymath} \vert H_n\vert^2 \end{displaymath}$

(10)

で与えられる．もとの関数が実数である場合には，周波数fと周波数-fのパワーは一致することに注意．

また, 離散逆フーリエ変換は次式で与えられる.

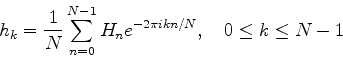$\begin{displaymath} h_k={1\over N}\sum_{n=0}^{N-1}H_ne^{-2\pi i kn/N}, \quad 0\le k\le N-1 \end{displaymath}$

(11)

練習問題2

$\displaystyle \sum_{n=0}^{N-1}e^{2\pi i n(k-k')/N}$	$\textstyle =$	$\displaystyle N \quad k=k'$
	$\textstyle =$	$\displaystyle 0 \quad {\rm else}$	(12)

を用いて, 式（9）から離散逆フーリエ変換の式（11）を導け.

練習問題3

このデータは，時間間隔Δt=0.209439(=2π/30)，時間領域 0< t < 2π において定数関数h(t)=1のデータである．データ数は３０である．このデータをセーブしてgnupotでグラフを作成せよ．
式（9）を元に, 離散フーリエ変換を行うプログラムを作成せよ. 結果のファイルに，周波数f （式６），パワー（実部**2+虚部**2）, 実部，虚部と並べて出力すること．上のデータを用いて離散フーリエ変換を行ってみよ．
どの周波数のパワーが強くなっているかをgnuplot でプロットすることによりそれぞれ確認せよ．
式（11）を元に, 離散フーリエ変換の結果を逆変換するプログラムを作成せよ. 結果のファイルに，時間，離散逆フーリエ変換成分の実部，虚部と並べて出力すること．
式（９）と（１２）からhk=1の場合の離散フーリエ変換を行ってみよ．数値計算の結果と比較せよ．

[3]三角関数の離散フーリエ変換

cos関数とsin関数

このデータは，cos(t) ( t=kΔt, Δt=2π/N, N=30, 0&le k &le 29)の値を出力したものである．データ数は３０である．このデータをセーブしてgnupotでグラフを作成せよ．離散フーリエ変換を行い

どの周波数のパワーが大きくなっているか

フーリエ成分の実部と虚部の大きさをそれぞれ確認せよ．なお，cos(t)の周波数は1/2πであることに注意すること．

また， sin(t) ( t=kΔt, Δt=2π/N, N=30, 0&le k &le 29)のデータについても行うこと．これらの結果から，cos関数のフーリエ成分は実部に値をもち，sin関数の場合は虚部に値を持つことがわかる．

sin関数その2

次に，sin(t)から位相がずれてsin(t+Δ) (t=kΔt, Δt=2π/N, N=30, 0&le k &le 29)となっている場合の離散フーリエ変換をおこなってみよ．

データをgnuplotで確認した上，離散フーリエ変換を行うこと．

sin(2πk/N+Δ)=sin(2πk/N)cos(Δ)+sin(Δ)cos(2πk/N)に注意すると，実部の大きさと虚部の大きさの比をとればtan(Δ)がわかる．このことから位相Δを決定せよ．

sin関数その3

このデータは，3つの三角関数の和を先ほどと同じ時間間隔，時間範囲で出力したものである．離散フーリエ変換を行い，3つの周波数を決定せよ．

[4]離散フーリエ変換の性質

ナイキストの臨界周波数

データ１は，sin(20t) (t=kΔt, Δt=2π/N, N=30, 0&le k &le 29)のデータである．この場合のナイキストの臨界周波数は，f_c=1/2Δt=15/2πとなる．sin(20t)の周波数は20/2πであるので臨界周波数よりも大きい．このデータの離散フーリエ変換を行い，どの周波数が強くなっているか確認せよ．
データ２は，h(t)=sin(50t)　(t=kΔt, Δt=2π/N, N=30, 0&le k &le 29)をサンプリングしたものである．gnuplotでデータ１と重ねてプロットしてみよ．
データ３は，h(t)=sin(10t)　(t=kΔt, Δt=2π/N, N=30, 0&le k &le 29)をサンプリングしたものである．この場合のh(t)の周波数は，10/2πとなるので臨界周波数よりも小さい．よって離散フーリエ変換は正しく行われる．パワーをデータ1のものとともにプロットさせてみよ．この結果から，データ1の離散フーリエ変換の結果は，2f_cだけずれたH_nが重なったものを見ていたことが分かる．

Δt,Nを変化させてみる

離散フーリエ変換においてΔtとNを変化させるとどうなるだろうか．データ4 は，Δt=2.09439(=2π/3)で 0&le t&le 10Δtでh(t)=1.，11Δt&le t&le 99Δtでh(t)=0.となっているデータである．データ5は，Δt=2.09439(=2π/3)で 0&le t&le 10Δtでh(t)=1.，11Δt&le t&le 49Δtでh(t)=0.である．どちらも矩形の関数でΔtは同一であるが，データの総数に違いがある．データ4のデータ数は100，データ5では50である．

二つのデータをgnuplotで確認せよ．
離散フーリエ変換を行い，振幅の分布をgnuplotで確認せよ．データの総数の違いは，周波数の分解能として現れることがわかる．

データ6は，Δt=1.04719(=2π/6)で 0&le t&le 20Δtでh(t)=1.，21Δt&le t&le 199Δtでh(t)=0.となっているデータである．つまり，データ１と比べるとΔtが1/2となっていてデータ総数は二倍となっている．

データ4とデータ6をgnuplotで確認せよ．
離散フーリエ変換を行い，データ4とデータ6の振幅の分布をgnuplotで確認せよ．Δtの違いは，周波数領域での折り返しの違いに現れる．ナイキストの臨界周波数が大きくなるほど，折り返しの効果は相対的に小さくなる．gnuplotで値の大きさを変化させてプロットするには，plot 'ファイル名' u 1:($2/2)　などとすればよい．

数値解析法及び演習 第十二回