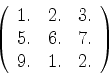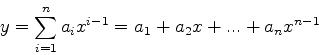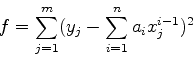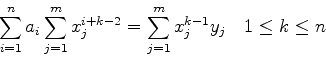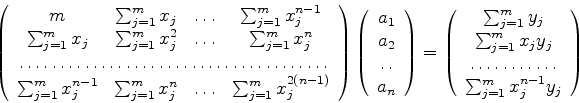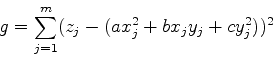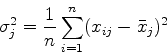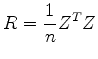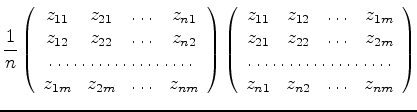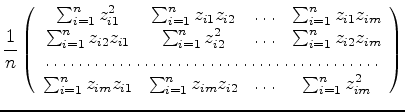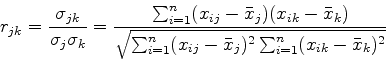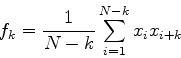数値解析法及び演習 第十一回

データ解析
  1. 逆行列を求めるサブルーチン
  2. 最小自乗法II
  3. 多変量の相関
  4. 自己相関
  5. 今日の宿題

[1] 逆行列を求めるサブルーチン

gasjo(a,n)
n次の正方行列a(n,n)を与えるとa(n,n)にその逆行列を返すサブルーチン．したがって代入したa(n,n)は失われる.

注意点：gasjoに代入する配列aのサイズはa(n,n+1)になっていること．メインプログラムでは同じサイズの配列を宣言しておかないとエラーになる． 


      subroutine gasjo(a,n)
      real*8 a(n,n+1),t
      integer ip(n),in(n,2)

      do j=1,n
      ip(j)=0
      enddo

      do 10 i=1,n

      t=0.D0
      do 66 j=1,n
       if(ip(j).eq.1) go to 66
        do 6 k=1,n
         if(ip(k).eq.1) go to 6
        ttx=abs(a(j,k))
        if(t.gt.ttx) go to 6
        ir=j
        ic=k
        t=ttx
    6 continue
 66   continue

      ip(ic)=1
      if(ir.eq.ic) go to 7

      do 8 l=1,n
      t=a(ir,l)
      a(ir,l)=a(ic,l)
      a(ic,l)=t
   8  continue

   7  in(i,1)=ir
      in(i,2)=ic
      pi=a(ic,ic)

      a(ic,ic)=1.D0
      do 9 l=1,n
      a(ic,l)=a(ic,l)/pi
   9  continue
  
      do 11 li=1,n
       if(li.eq.ic) go to 11
       t=a(li,ic)
       a(li,ic)=0.D0
       do 12 l=1,n
       a(li,l)=a(li,l)-a(ic,l)*t
   12 continue
   11 continue

   10 continue

      do 133 i=1,n
      l=n-i+1
       if(in(l,1).eq.in(l,2)) go to 133
        jr=in(l,1)
        jc=in(l,2)
        do 13 k=1,n
        t=a(k,jr)
        a(k,jr)=a(k,jc)
        a(k,jc)=t
   13  continue
 133   continue
       return
       end

練習問題1

上に与えたサブルーチンgasjo(a,n)を用いて以下の行列の逆行列を求めよ．も との行列との積をとり，正しく単位行列になるかかチェックもせよ．


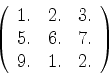\begin{displaymath} \left( \begin{array}{ccc} 1. & 2. & 3.\\ 5. & 6. & 7.\\ 9. & 1. & 2. \end{array}\right) \end{displaymath} (1)

練習問題2

次の連立方程式をさきほどのサブルーチンを用いて解け.


$\displaystyle 5.x+2.y+6.z$ $\textstyle =$ $\displaystyle 7.$  
$\displaystyle 2.x+2.8y+4.4z$ $\textstyle =$ $\displaystyle 7.8$ (2)
$\displaystyle 4.x+3.y+8.2z$ $\textstyle =$ $\displaystyle 6.$  

練習問題3

プログラム中で単位行列を作成せよ．その逆行列を求めよ（答えは単位行列）．行列のサイズを10から1000程度まで変化させ，行列のサイズとともに，計算時間がどう変化するか観察せよ．計算時間は 

time ./a.out
とtimeコマンドを使用することで表示できる．

[2]最小自乗法II

それでは逆行列のアルゴリズムを使う練習を行う．

またまた最小自乗法をとりあげる．いままでに行ったのは，フィッティングす る関数を


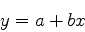\begin{displaymath} y=a+bx \end{displaymath} (3)

と線形に仮定してきた．今度は多項式


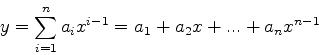\begin{displaymath} y=\sum_{i=1}^{n}a_ix^{i-1}=a_1+a_2x+...+a_nx^{n-1} \end{displaymath} (4)

を仮定する．ここで実験データがmこあるとすると，多項式の項数はm以下でな ければならない(式の数が足りなくなるから)．

ここで係数aを決定するのが仕事となる．以前と同じように，関数のフィッティングは


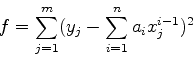\begin{displaymath} f=\sum_{j=1}^m(y_j-\sum_{i=1}^{n}a_ix_j^{i-1})^2 \end{displaymath} (5)

を最小にすることで行う．そのためにはfを各aで偏微分してゼロにすれば良い．


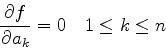\begin{displaymath} {\partial f\over \partial a_k}=0 \quad 1\le k \le n \end{displaymath} (6)

これを計算すると


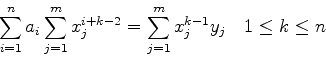\begin{displaymath} \sum_{i=1}^{n}a_i\sum_{j=1}^m x_j^{i+k-2}=\sum_{j=1}^mx_j^{k-1}y_j \quad 1\le k \le n \end{displaymath} (7)

という連立方程式を解くことになる．行列の形で書き替えると


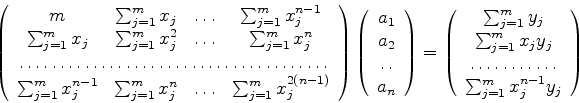\begin{displaymath} \left( \begin{array}{cccc} m & \sum_{j=1}^m x_j & \ldots & \... ...c}{\dotfill}\\ \sum_{j=1}^m x_j^{n-1} y_j \end{array}\right) \end{displaymath} (8)

となる．

練習問題4

逆行列をもとめるアルゴリズムを用いて 
x  y

1.D0 3.D0
3.D0 6.D0
5.D0 5.5D0
7.D0 5.D0
9.D0 7.D0
を二次式，三次式でフィッティングせよ．

練習問題5

このデータはある曲面から作成したものである．データを保存してgnuplotを実行し， 
splot 'kyokumen.dat'
で曲面の形状を確認せよ．曲面の形状を


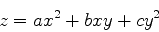\begin{displaymath} z=ax^2+bxy+cy^2 \end{displaymath} (9)

と仮定し，データをフィッティングするa,b,cを決定せよ．a+cは平均曲率，4ac-bはガウス曲率と呼ばれる．先ほどと同様に，


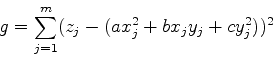\begin{displaymath} g=\sum_{j=1}^m(z_j-(ax_j^2+bx_jy_j+cy_j^2))^2 \end{displaymath} (10)

を最小にするために


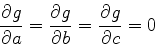\begin{displaymath} {\partial g\over \partial a}={\partial g\over \partial b}={\partial g\over \partial c}=0 \end{displaymath} (11)

から構成される連立方程式を解けばよい．

[4] 多変量の相関

いくつかの特性に対するデータが得られたときそれをどう味わうかを考える． ここでは多変量の相関を考える．例として以下のデータをみてみよう．


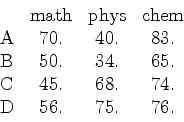\begin{displaymath} \begin{array}{cccc} & {\rm math} & {\rm phys}& {\rm chem} \... ... C} & 45. & 68. & 74.\\ {\rm D} & 56. & 75. & 76. \end{array}\end{displaymath} (12)

このように，サンプル(Aさん，Bさん．．)を行にとり，変量(数学，理科．．)を列 にとって作った測定値の行列をデータ行列と呼ぶ．多変量解析の目的は, どの変量とどの変量が相互に関係しているのかを統計的に推測することである.

一般に異なる変量は異なる次元を持つ．そのためまず各変量をおなじように扱 えるようにするために標準化という作業をおこなう．これは，平均値がゼロ， 分散が1となるような変換をデータに施すことである．ある変量の平均値は


\begin{displaymath} \bar{x}_j={1\over n}\sum_{i=1}^nx_{ij} \end{displaymath} (13)

であたえられる．分散（標準偏差の二乗）は
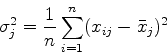\begin{displaymath} \sigma_j^2={1\over n}\sum_{i=1}^n(x_{ij}-\bar{x}_j)^2 \end{displaymath} (14)

となる．データの標準化は


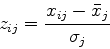\begin{displaymath} z_{ij}={x_{ij}-\bar{x}_j\over \sigma_j} \end{displaymath} (15)

の変換によっておこなわれる．この変換をおこなった行列を標準化行列と呼ぶ．標準化の結果, 平均値が0, 分散が1となる.


\begin{displaymath} Z= \left( \begin{array}{cccc} z_{11} & z_{12} & \ldots & z_{... ...fill}\\ z_{n1} & z_{n2} & \ldots & z_{nm} \end{array}\right) \end{displaymath} (16)

ここでこの行列の転置行列をかけると


$\displaystyle R={1\over n}Z^{T}Z$ $\textstyle =$ $\displaystyle {1\over n} \left( \begin{array}{cccc} z_{11} & z_{21} & \ldots & ... ...icolumn{4}{c}{\dotfill}\\ z_{n1} & z_{n2} & \ldots & z_{nm} \end{array}\right)$  
  $\textstyle =$ $\displaystyle {1\over n}\left( \begin{array}{cccc} \sum_{i=1}^{n} z_{i1}^2 & \s... ...um_{i=1}^{n} z_{im}z_{i2} & \ldots & \sum_{i=1}^{n} z_{im}^2 \end{array}\right)$ (17)

となり各要素は二つの変量の間の相関係数を与える．変量jと変量kの相関係数は


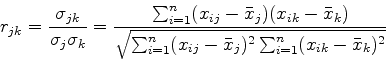\begin{displaymath} r_{jk}={\sigma_{jk}\over \sigma_j\sigma_k} ={\sum_{i=1}^n(x_... ..._{i=1}^n(x_{ij}-\bar{x}_j)^2\sum_{i=1}^n(x_{ik}-\bar{x}_k)^2}} \end{displaymath} (18)

であたえられる．二つの変量の相関がよいほど相関係数の値の絶対値は1に近 くなる．行列Rの要素はそれぞれ二つの変量の相関係数のため，Rは相関行列と 呼ばれる． それではでて来た相関係数はどう味わえばよいのか？ それには次の表を用いる. Nはデータの数, rは相関係数である. それぞれの数値は, 無相関のN個のデータがあった時にr以上の相関係数が出現する確率（パーセント）である. この数値が小さい程, 二つのデータには相関があると思ってよい. 5以下なら有意, 1以下なら高度に有意であるという.
r
N 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0
3 100 94 87 81 74 67 59 51 41 29 0
6 100 85 70 56 43 31 21 12 6 1 0
10 100 78 58 40 25 14 7 2 0.5 0
20 100 67 40 20 8 2 0.5 0.1 0
50 100 49 16 3 0.4 0

無相関な二つの量がN組あったとき, 相関係数がr以上になる確率. 空白は0.05%以下.

練習問題6

「健康診断データ」，「大手私鉄データ」，「株式，為替レートデータ」，「体力測定データ」を解析し，どの項目とどの項目に高度に有意な相関があるか指摘せよ．

[4] 自己相関

前節では「異なる量」の間の相関を考えた．今度は自分自身との相関を考えてみる．

ある時系列データxi (1&le i &le N)がある．この量の自己相関関数は次式で定義することができる．


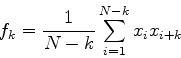\begin{displaymath} f_{k}={1\over N-k}\sum_{i=1}^{N-k}x_i x_{i+k} \end{displaymath} (19)

練習問題7

練習問題8

「伊豆大島における常時微小振動データ」の自己相関関数を式(19)に従って計算せよ．0&le k &le 2000　まで変化させて横軸k, 縦軸fk のグラフを作成せよ．このデータはサンプリングレート100Hzで一時間である（データの総数は360000）．左列は時間，右列が振幅．したがって，このグラフの横軸を1/100すると秒となる．2秒以降にピークは見られるか？　その意味はなんだろう？

今日の宿題 (12/15日まで)




日程表へ戻る <<