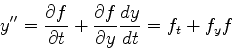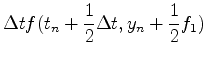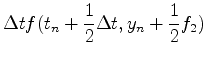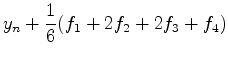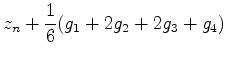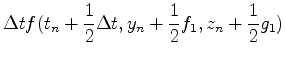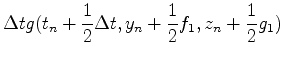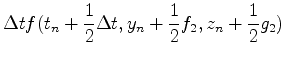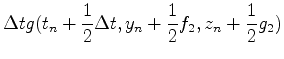数値解析法及び演習 第八回

常微分方程式1
  1. 関数副プログラム
  2. オイラー法
  3. オイラー法
  4. Δtの二次の精度
  5. ルンゲクッタ法
  6. 連立1階微分方程式
  7. 今日の宿題

[1]関数副プログラム

フォートランにはデフォルトでいくつかの関数が用意されているが，ユーザー が独自に関数を定義して用いたい場合は「関数副プログラム」というものをつかって関数を定義することが出来る．使い方は 

t function f(a1,a2,....aN)
......
f=.....
return
end
function文 f=.... 関数副プログラムの定義をおこなう
t 型宣言：real*8, integerなど
a1,a2,...aN 仮引数：型宣言をすること
プログラム中で用いる時は, 
b=f(c1,c2,....cn)
のように引数を代入して行う．

たとえば, 1からnまでの総和を求める関数副プログラムは 

      integer function souwa(n)
      implicit none
      integer i,n

      souwa=0
      do i=1,n
      souwa=souwa+i
      enddo
      return
      end

      
      implicit none
      integer souwa,n
      read(5,*) n
      write(6,*) souwa(n)
      end

注意点

練習問題1

1) n!を計算する関数副プログラム fact(n)を作成せよ．
2) n個のものからm個のものを取り出す組み合わせの数 nCmを計算する関数副 プログラムを作成せよ．
3) 二項定理によると，f(x,y,n)=(x+y)**nは
(x+y)**n=ΣnCm x**(n-m)y**m
となる．f(x,y,n)を計算する関数副プログラムを作り，x=0.3,y=0.7,n=10として実行し，結果が1.0になることを確かめよ．

[2] オイラー法

一階の常微分方程式


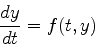\begin{displaymath} {dy\over dt}=f(t,y) \end{displaymath} (1)

を初期条件 t=t0 のとき y=y0 のもとで解くことを考える．tをtn=t0+n△tと△ tづつ増加させるとき，n回目の値 yn=y(tn)を順に求めていく．
最も単純な方法は，


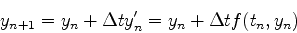\begin{displaymath} y_{n+1}=y_n+\Delta t y_n'=y_n+\Delta t f(t_n,y_n) \end{displaymath} (2)

としてどんどん足し算していく方法である．これをオイラー法と呼ぶ．

練習問題2

次の常微分方程式
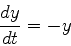\begin{displaymath} {dy\over dt}=-y \end{displaymath} (3)

を初期条件t=0のときy=1のもとでt=2まで解き，解析的に得られる解


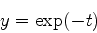\begin{displaymath} y=\exp(-t) \end{displaymath} (4)

と比較せよ．時間刻みを変化させて(1.D-1, 1.D-2, 1.D-3)誤差の変化を観察せよ．

[3]常微分方程式その2 「Δtの二次の精度」

オイラー法における誤差はΔtに比例する(一ステップの誤差はΔtの二乗に比例するため)．すな わち誤差を10分の1にしたければΔtを1/10にする必要がある．これは計算にかか る時間が10倍になることを意味する．これでは時間がかかってしょうがない． そこでΔtの2乗，4乗に誤差が比例するようなアルゴリズムが存在する．4乗に 比例するものはルンゲクッタ法と呼ばれ広く用いられている．

ルンゲクッタ法に入る前に誤差がΔtの2乗に比例するアルゴリズムについて考 えてみよう．


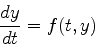\begin{displaymath} {dy\over dt}=f(t,y) \end{displaymath} (5)

という微分方程式が与えられたものとする．タイムステップがΔtのとき，n+1 ステップ目のyの値yn+1は，ynを用いて
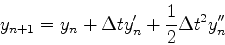\begin{displaymath} y_{n+1}=y_n+\Delta t y_n'+{1\over 2}\Delta t^2 y_n'' \end{displaymath} (6)

と書くことができる．ここでy''は二次の微係数で
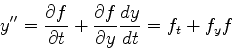\begin{displaymath} y''={\partial f\over \partial t}+{\partial f\over \partial y}{dy\over dt} =f_t+f_yf \end{displaymath} (7)

となる．2項出てくることに注意．これを用いると先ほどの式は


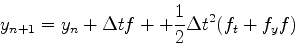\begin{displaymath} y_{n+1}=y_n+\Delta t f++{1\over 2}\Delta t^2 (f_t+f_yf) \end{displaymath} (8)

のようにかきかえられる．ここでポイントは，我々はft,fyを知らないと言うことである．なので別の式でさらに書き替えないといけない．そのため式(8)が，以下のように書けるものと仮定する．


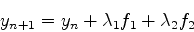\begin{displaymath} y_{n+1}=y_n+\lambda_1f_1+\lambda_2f_2 \end{displaymath} (9)

ここでf1，f2は


$\displaystyle f_1$ $\textstyle =$ $\displaystyle \Delta t f(t_n,y_n)$ (10)
$\displaystyle f_2$ $\textstyle =$ $\displaystyle \Delta t f(t_n+\alpha\Delta t,y_n+\beta k_1)$ (11)

である．f2の中身に注意．f1，f2はそれぞれtnでの傾き，および傾きk1でΔt 秒進んだとしたときのt+Δt秒後の傾きを表す．この二つの傾きを適当に重ね 合わせることによりΔtの二乗の精度にすることができる．(11)式をテーラー展 開すると，λ1，λ2，α，βの間の関係式が


$\displaystyle \lambda_1+\lambda_2$ $\textstyle =$ $\displaystyle 1$ (12)
$\displaystyle \lambda_1\alpha$ $\textstyle =$ $\displaystyle {1\over 2}$ (13)
$\displaystyle \lambda_2\beta$ $\textstyle =$ $\displaystyle {1\over 2}$ (14)

と求めることができる．求めるべき数が4つあるのに式が３つしか存在しない．なのでいろいろな値の組み合わせが


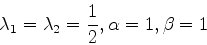\begin{displaymath} \lambda_1=\lambda_2={1\over 2}, \alpha=1, \beta=1 \end{displaymath} (15)


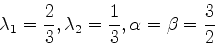\begin{displaymath} \lambda_1={2\over 3}, \lambda_2={1\over 3}, \alpha=\beta={3\over 2} \end{displaymath} (16)

といったようにありうる．いずれの場合も二次の精度まで正しく計算できる．つまり一ステップの誤差はΔtの3乗に比例する. 今回は(15)式を採用し，以下の(17)-(19)式で積分を行う．


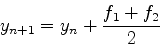\begin{displaymath} y_{n+1}=y_n+{f_1+f_2\over 2} \end{displaymath} (17)


$\displaystyle f_1$ $\textstyle =$ $\displaystyle \Delta t f(t_n,y_n)$ (18)
$\displaystyle f_2$ $\textstyle =$ $\displaystyle \Delta t f(t_n+\Delta t,y_n+f_1)$ (19)

練習問題3

式(17),(18),(19)を用いて，上で解説した方法を用いて先の例の積分を行 え．オイラー法の場合と精度を比較せよ．

[4] ルンゲクッタ法

先ほどのアルゴリズムの誤差はΔtの二乗である．これを4乗に高めたの がルンゲクッタ法である．

さきほどと同じ考え方を使うと，ルンゲクッタ法のアルゴリズムは以下のよう になる．


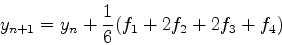\begin{displaymath} y_{n+1}=y_n+{1\over 6}({f_1+2f_2+2f_3+f_4}) \end{displaymath} (20)


$\displaystyle f_1$ $\textstyle =$ $\displaystyle \Delta t f(t_n,y_n)$  
$\displaystyle f_2$ $\textstyle =$ $\displaystyle \Delta t f(t_n+{1\over 2}\Delta t,y_n+{1\over 2}f_1)$  
$\displaystyle f_3$ $\textstyle =$ $\displaystyle \Delta t f(t_n+{1\over 2}\Delta t,y_n+{1\over 2}f_2)$  
$\displaystyle f_4$ $\textstyle =$ $\displaystyle \Delta t f(t_n+\Delta t,y_n+f_3)$ (21)

練習問題3

式(20),(21)を用いて，ルンゲクッタ法を用いて先の例の積分を行え．３つの 場合の誤差を比較せよ．

[4] 連立微分方程式

先ほどのルンゲクッタ法は多変数に拡張できる．例えば，y=y(t)とz=z(t)がそれぞれ


$\displaystyle {dy\over dt}$ $\textstyle =$ $\displaystyle f(t,y,z)$  
$\displaystyle {dz\over dt}$ $\textstyle =$ $\displaystyle g(t,y,z)$ (22)

にしたがって進化する場合は，以下のようにアルゴリズムを組めばよい．


$\displaystyle y_{n+1}$ $\textstyle =$ $\displaystyle y_n+{1\over 6}(f_1+2f_2+2f_3+f_4)$  
$\displaystyle z_{n+1}$ $\textstyle =$ $\displaystyle z_n+{1\over 6}(g_1+2g_2+2g_3+g_4)$ (23)


$\displaystyle f_1$ $\textstyle =$ $\displaystyle \Delta t f(t_n,y_n,z_n)$  
$\displaystyle g_1$ $\textstyle =$ $\displaystyle \Delta t g(t_n,y_n,z_n)$ (24)


$\displaystyle f_2$ $\textstyle =$ $\displaystyle \Delta t f(t_n+{1\over 2}\Delta t,y_n +{1\over 2}f_1,z_n+{1\over 2}g_1)$  
$\displaystyle g_2$ $\textstyle =$ $\displaystyle \Delta t g(t_n+{1\over 2}\Delta t,y_n +{1\over 2}f_1,z_n+{1\over 2}g_1)$ (25)


$\displaystyle f_3$ $\textstyle =$ $\displaystyle \Delta t f(t_n+{1\over 2}\Delta t,y_n +{1\over 2}f_2,z_n+{1\over 2}g_2)$  
$\displaystyle g_3$ $\textstyle =$ $\displaystyle \Delta t g(t_n+{1\over 2}\Delta t,y_n +{1\over 2}f_2,z_n+{1\over 2}g_2)$ (26)


$\displaystyle f_4$ $\textstyle =$ $\displaystyle \Delta t f(t_n+\Delta t,y_n+f_3,z_n+g_3)$  
$\displaystyle g_4$ $\textstyle =$ $\displaystyle \Delta t g(t_n+\Delta t,y_n+f_3,z_n+g_3)$ (27)

練習問題5


$\displaystyle {dx\over dt}$ $\textstyle =$ $\displaystyle f(t,x,y)=\omega y$  
$\displaystyle {dy\over dt}$ $\textstyle =$ $\displaystyle g(t,x,y)=-\omega x$ (28)

式(28)で与えられる連立微分方程式を解け．なお，ω=1.D0とせよ．t=0.D0でx=0.D0, y=1.D0とする．

[6] 今日の宿題 (11/24日まで)

  1. 練習問題4のプログラム, および3つの方法（オイラー法，二次精度，ルンゲクッタ法）それぞれの誤差.
  2. 練習問題5のプログラム



日程表へ戻る <<