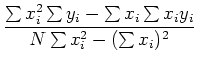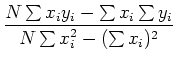数値解析法及び演習第四回

[1] gnuplotの基本

gnuplot(ニュープロットとよむ)は，UNIXシステムにおける簡便なグラフ描画ソフトである．起動は

gnuplot

で行われる．
最も基本的なデータは

-1.0   -3.2
 0.0   -0.9
 1.0    1.2
 2.0    2.8
 3.0    5.0

といった形で与えられる．左側のデータをx座標，右側のデータ(ファイル名を plot.datとする)をy座標とおもってxy平面上にプロットするときは，gnuplotを起動した画面で

plot 'plot.dat'

とするとグラフが描かれる．さらに

plot 'plot.dat' w l

とするとデータ点を線で結ぶ．また，gnuplotにはいろいろな関数が用意されていて，

plot sin(x)

とするとサインカーブを描いてくれる．他にもワザはたくさんあり GNUPLOT入門（kawanoさんのページ）等に出ているので参考にしてください．

二つの量を測定したときに，そのあいだに線形の関係が期待されることがよくある．もっともありそうな傾き(B)と切片(A)を求めるのが最小二乗法である．最小二乗法の解説

最小二乗法では, 測定されたデータの組(x,y)にフィットする直線を求める. データxは正確に求められているとし, またデータyのバラツキは正規分布をしているものとする. この場合, フィットする直線をy=A+Bxとすると, A,Bはそれぞれ

$\displaystyle A$	$\textstyle =$	$\displaystyle {\sum x_i^2\sum y_i-\sum x_i\sum x_i y_i\over N\sum x_i^2-(\sum x_i)^2}$
$\displaystyle B$	$\textstyle =$	$\displaystyle {N\sum x_iy_i-\sum x_i\sum y_i\over N\sum x_i^2-(\sum x_i)^2}$

となる. したがって切片Aと傾きBを算出するためには次の和をもとめればよい．

次のx，yのデータをファイルから読み込ませ，最小二乗法によりフィットした直線の傾きと切片を求めるプログラムを作成せよ. AとBを求めたら, その直線とデータをgnuplotで描き, フィッテイングが正しいことを確かめよ.


-1.0   -3.2
 0.0   -0.9
 1.0    1.2
 2.0    2.8
 3.0    5.0

プログラム中で条件分岐を行いたいときはIF文を用いる．基本の形を以下にしめす．

例1：

if(b) 実行文

bには論理式または算術関係式がはいります（算術関係式は下に説明. 論理式は後日説明します. ）．この形式だとbが真の場合にのみ実行文が行われ，それ以外だと何もせず次に制御が移ることになります．

例2:

if(b) then
実行文 
endif

基本的に上とおなじ. 実行文が二行以上になる時.

例3:

if(b) then

実行文 1

else

実行文 2

endif

上の形式では，もしbが真であれば実行文1が行われ，偽であれば実行文2が行われます．実行文2にもあてはまらない場合をさらに場合分けしたいときはさらにブロックを重ねることができます.

if(b) then

実行文 1

else if(c) then

実行文 2

else

実行文3

endif

この場合は, もしbが真であれば実行文1が行なわれます. 偽の場合はさらにcによって条件がわかれ, 真の場合は2が, 偽の場合は3が実行されます. このif-elseブロックはいくらでも重ねることができます.

たとえば，以下のプログラムはキーボードから入力した値が10.以上ならその値を画面に表示させるプログラムである．

      implicit none      
      real*8 a

      read(5,*) a
      if(a.ge.1.D1) then
      write(6,*) a
      endif

      end

このプログラムを作成して実行してみよ．

さきほどの10個の整数を大きい順に並び変えモニタに表示するプログラムを作成せよ.
キーボードから整数を一つ入力し，その整数が素数であればその数を，素数で無ければその数の2倍をモニタに表示するプログラムを作成せよ．ヒント：mod(k,i)関数は，kをiで割った余りを返す関数である．

〆切は10/27. すべてのプログラムを添付ファイルで送付すること（結果はいらない）．

日程表へ戻る << 　