[1]モンテカルロ法
乱数を用いると多重積分を容易に行うことができる.例としてN次元単位球の体積を求めてみよう.
乱数をN個用意する.各乱数 xi (1≤i≤N) は0から1の値をとる.この乱数の組をW回生成する.生成した乱数のうち,
| (1) |
| (2) |
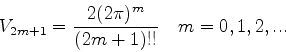 |
(3) |
| (4) |
練習問題1
- N=2の場合について,W=10, 102, 103, 104と変化させて誤差の変化を観察せよ.
- W=104とし,N=1〜10までについて体積を算出せよ.体積はどう変化したか?
乱数を用いると多重積分を容易に行うことができる.例としてN次元単位球の体積を求めてみよう.
乱数をN個用意する.各乱数 xi (1≤i≤N) は0から1の値をとる.この乱数の組をW回生成する.生成した乱数のうち,
| (1) |
| (2) |
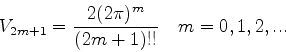 |
(3) |
| (4) |
注意点:gasjoに代入する配列aのサイズはa(n,n+1)になっていること.メインプログラムでは同じサイズの配列を宣言しておかないとエラーになる.
subroutine gasjo(a,n)
real*8 a(n,n+1),t
integer ip(n),in(n,2)
do j=1,n
ip(j)=0
enddo
do 10 i=1,n
t=0.D0
do 66 j=1,n
if(ip(j).eq.1) go to 66
do 6 k=1,n
if(ip(k).eq.1) go to 6
ttx=abs(a(j,k))
if(t.gt.ttx) go to 6
ir=j
ic=k
t=ttx
6 continue
66 continue
ip(ic)=1
if(ir.eq.ic) go to 7
do 8 l=1,n
t=a(ir,l)
a(ir,l)=a(ic,l)
a(ic,l)=t
8 continue
7 in(i,1)=ir
in(i,2)=ic
pi=a(ic,ic)
a(ic,ic)=1.D0
do 9 l=1,n
a(ic,l)=a(ic,l)/pi
9 continue
do 11 li=1,n
if(li.eq.ic) go to 11
t=a(li,ic)
a(li,ic)=0.D0
do 12 l=1,n
a(li,l)=a(li,l)-a(ic,l)*t
12 continue
11 continue
10 continue
do 133 i=1,n
l=n-i+1
if(in(l,1).eq.in(l,2)) go to 133
jr=in(l,1)
jc=in(l,2)
do 13 k=1,n
t=a(k,jr)
a(k,jr)=a(k,jc)
a(k,jc)=t
13 continue
133 continue
return
end
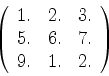 |
(5) |
次の連立方程式をさきほどのサブルーチンを用いて解け.
| (6) | |||
プログラム中で単位行列を作成せよ.その逆行列を求めよ(答えは単位行列).行列のサイズを10から1000程度まで変化させ,計算時間がどう変化するか観察せよ.計算時間は
time ./a.outとtimeコマンドを使用することで表示できる.
それでは逆行列のアルゴリズムを使う練習を行う.
またまた最小自乗法をとりあげる.いままでに行ったのは,フィッティングす る関数を
| (7) |
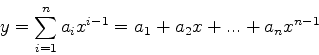 |
(8) |
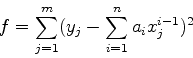 |
(9) |
| (10) |
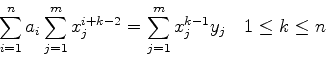 |
(11) |
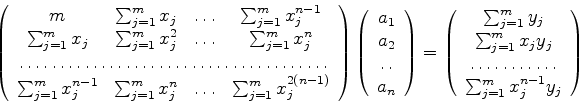 |
(12) |
x y 1.D0 3.D0 3.D0 6.D0 5.D0 5.5D0 7.D0 5.D0 9.D0 7.D0を二次式,三次式でフィッティングせよ.
splot 'kyokumen.dat'で曲面の形状を確認せよ.曲面の形状を
| (13) |
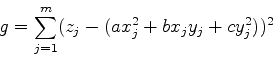 |
(14) |
| (15) |
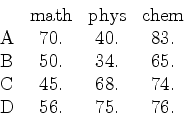 |
(16) |
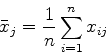 |
(17) |
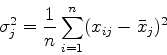 |
(18) |
| (19) |
 |
(20) |
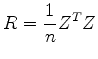 |
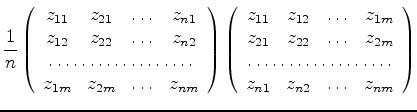 |
||
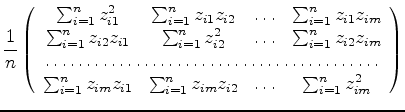 |
(21) |
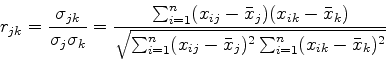 |
(22) |
| r | |||||||||||
| N | 0.0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1.0 |
| 3 | 100 | 94 | 87 | 81 | 74 | 67 | 59 | 51 | 41 | 29 | 0 |
| 6 | 100 | 85 | 70 | 56 | 43 | 31 | 21 | 12 | 6 | 1 | 0 |
| 10 | 100 | 78 | 58 | 40 | 25 | 14 | 7 | 2 | 0.5 | 0 | |
| 20 | 100 | 67 | 40 | 20 | 8 | 2 | 0.5 | 0.1 | 0 | ||
| 50 | 100 | 49 | 16 | 3 | 0.4 | 0 |
無相関な二つの量がN組あったとき, 相関係数がr以上になる確率. 空白は0.05%以下.
以下の問題に回答せよ.
「健康診断データ」,「大手私鉄データ」,「株式,為替レートデータ」,「体力測定データ」を解析し,どの項目とどの項目に高度に有意な相関があるか指摘せよ.