[1]ガウス分布
ある量を繰り返し計測すると,計測値は特定の分布をとることが多い.分布の中でも特に重要なものはガウス分布(正規分布)である.
| (1) |
式(1)において,σ2は分散である.
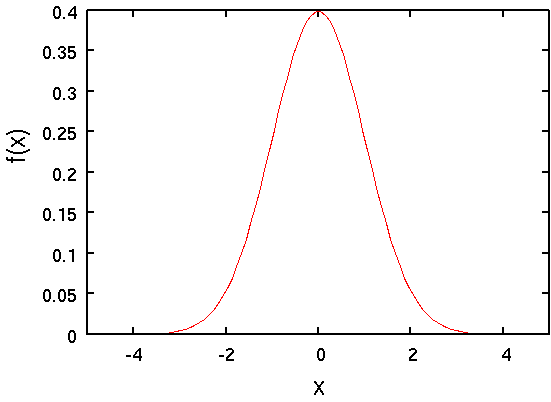 ガウス分布の図(平均値=1,分散=1)
ガウス分布の図(平均値=1,分散=1)
ガウス分布に近い計測値の例(新しい誤差論:古澤康和著より作成):
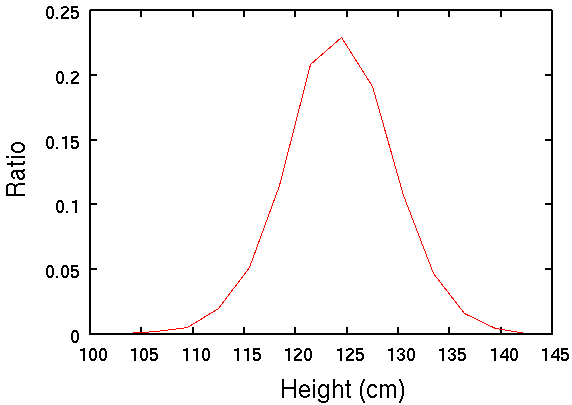
生徒の身長の分布.
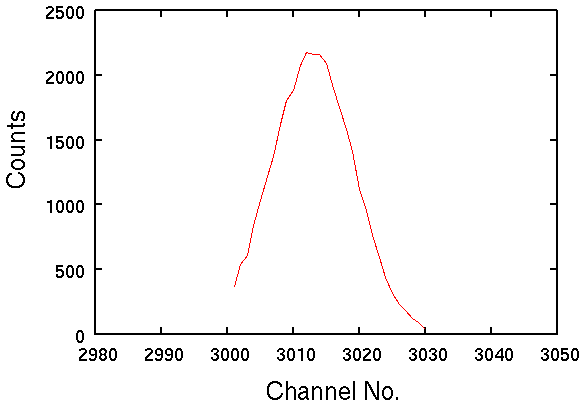
セシウム原子から放出されるガンマ線の計測結果.横軸はチャネル数,縦軸は計数値.
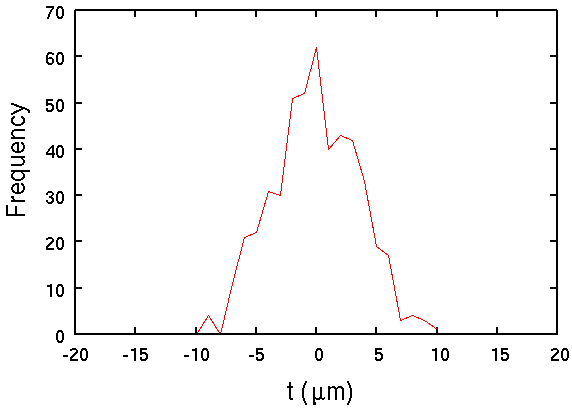
スペクトル線の位置の平均値からのずれ.横軸は残差でμm単位.
ある量を繰り返し計測すると,計測値は特定の分布をとることが多い.分布の中でも特に重要なものはガウス分布(正規分布)である.
| (1) |
式(1)において,σ2は分散である.
 ガウス分布の図(平均値=1,分散=1)
ガウス分布の図(平均値=1,分散=1)
ガウス分布に近い計測値の例(新しい誤差論:古澤康和著より作成):

生徒の身長の分布.

セシウム原子から放出されるガンマ線の計測結果.横軸はチャネル数,縦軸は計数値.

スペクトル線の位置の平均値からのずれ.横軸は残差でμm単位.
| (2) |
I=843314861*I+453816693
if(I.lt.0) I=(I+2147483647)+1
ran=float(I)*4.656612873D-10
をつかうことで[0,1)に規格化された乱数をつくることができる.乱数を用いると多重積分を容易に行うことができる.例としてN次元単位球の体積を求めてみよう.
乱数をN個用意する.各乱数 xi (1≤i≤N) は0から1の値をとる.この乱数の組をW回生成する.生成した乱数のうち,
| (3) |
| (4) |
 |
(5) |
| (6) |