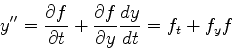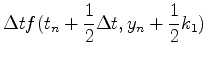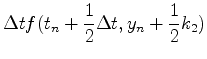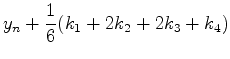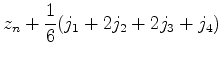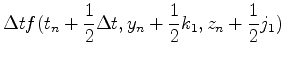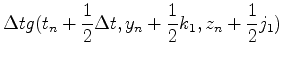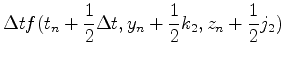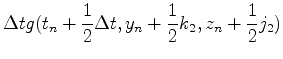数値解析法及び演習第八回

[1] オイラー法

一階の常微分方程式

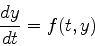$\begin{displaymath} {dy\over dt}=f(t,y) \end{displaymath}$

(1)

を初期条件 t=t0 のとき y=y0 のもとで解くことを考える．tをtn=t0+n△tと△ tづつ増加させるとき，n回目の値 yn=y(tn)を順に求めていく．
最も単純な方法は，

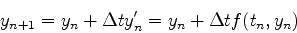$\begin{displaymath} y_{n+1}=y_n+\Delta t y_n'=y_n+\Delta t f(t_n,y_n) \end{displaymath}$

(2)

としてどんどん足し算していく方法である．これをオイラー法と呼ぶ．

練習問題1

次の常微分方程式

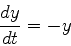$\begin{displaymath} {dy\over dt}=-y \end{displaymath}$ (3)

を初期条件t=0のときy=1のもとで解き，解析的に得られる解

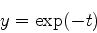$\begin{displaymath} y=\exp(-t) \end{displaymath}$

(4)

と比較せよ．t=2まで積分し，時間刻みを変化させて(1.D-1, 1.D-2, 1.D-3)誤差の変化を観察せよ．

[2]常微分方程式その2 「Δtの二次の精度」

オイラー法における誤差はΔtに比例する(一ステップの誤差はΔtの二乗に比例するため)．すなわち誤差を10分の1にしたければΔtを1/10にする必要がある．これは計算にかかる時間が10倍になることを意味する．これでは時間がかかってしょうがない．そこでΔtの2乗，4乗に誤差が比例するようなアルゴリズムが存在する．4乗に比例するものはルンゲクッタ法と呼ばれ広く用いられている．

ルンゲクッタ法に入る前に誤差がΔtの2乗に比例するアルゴリズムについて考えてみよう．

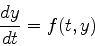$\begin{displaymath} {dy\over dt}=f(t,y) \end{displaymath}$

(5)

という微分方程式が与えられたものとする．タイムステップがΔtのとき，n+1 ステップ目のyの値yn+1は，ynを用いて

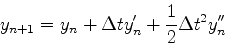$\begin{displaymath} y_{n+1}=y_n+\Delta t y_n'+{1\over 2}\Delta t^2 y_n'' \end{displaymath}$

(6)

と書くことができる．ここでy''は二次の微係数で

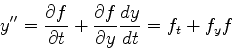$\begin{displaymath} y''={\partial f\over \partial t}+{\partial f\over \partial y}{dy\over dt} =f_t+f_yf \end{displaymath}$

(7)

となる．2項出てくることに注意．これを用いると先ほどの式は

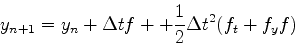$\begin{displaymath} y_{n+1}=y_n+\Delta t f++{1\over 2}\Delta t^2 (f_t+f_yf) \end{displaymath}$

(8)

のようにかきかえられる．ここでポイントは，我々はft,fyを知らないと言うことである．なので別の式でさらに書き替えないといけない．そのため式(8)が，以下のように書けるものと仮定する．

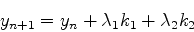$\begin{displaymath} y_{n+1}=y_n+\lambda_1k_1+\lambda_2k_2 \end{displaymath}$

(9)

練習問題2

[3] ルンゲクッタ法

先ほどのアルゴリズムの誤差はΔtの二乗である．これを4乗に高めたのがルンゲクッタ法である．

さきほどと同じ考え方を使うと，ルンゲクッタ法のアルゴリズムは以下のようになる．

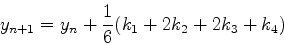$\begin{displaymath} y_{n+1}=y_n+{1\over 6}({k_1+2k_2+2k_3+k_4}) \end{displaymath}$

(20)

$\displaystyle k_1$	$\textstyle =$	$\displaystyle \Delta t f(t_n,y_n)$
$\displaystyle k_2$	$\textstyle =$	$\displaystyle \Delta t f(t_n+{1\over 2}\Delta t,y_n+{1\over 2}k_1)$
$\displaystyle k_3$	$\textstyle =$	$\displaystyle \Delta t f(t_n+{1\over 2}\Delta t,y_n+{1\over 2}k_2)$
$\displaystyle k_4$	$\textstyle =$	$\displaystyle \Delta t f(t_n+\Delta t,y_n+k_3)$	(21)

練習問題3

式(20),(21)を用いて，ルンゲクッタ法を用いて先の例の積分を行え．３つの場合の誤差を比較せよ．

[4] 連立微分方程式

先ほどのルンゲクッタ法は多変数に拡張できる．例えば，y=y(t)とz=z(t)がそれぞれ

$\displaystyle {dy\over dt}$	$\textstyle =$	$\displaystyle f(t,y,z)$
$\displaystyle {dz\over dt}$	$\textstyle =$	$\displaystyle g(t,y,z)$	(22)

にしたがって進化する場合は，以下のようにアルゴリズムを組めばよい．

$\displaystyle y_{n+1}$	$\textstyle =$	$\displaystyle y_n+{1\over 6}(k_1+2k_2+2k_3+k_4)$
$\displaystyle z_{n+1}$	$\textstyle =$	$\displaystyle z_n+{1\over 6}(j_1+2j_2+2j_3+j_4)$	(23)

$\displaystyle k_1$	$\textstyle =$	$\displaystyle \Delta t f(t_n,y_n,z_n)$
$\displaystyle j_1$	$\textstyle =$	$\displaystyle \Delta t g(t_n,y_n,z_n)$	(24)

$\displaystyle k_2$	$\textstyle =$	$\displaystyle \Delta t f(t_n+{1\over 2}\Delta t,y_n +{1\over 2}k_1,z_n+{1\over 2}j_1)$
$\displaystyle j_2$	$\textstyle =$	$\displaystyle \Delta t g(t_n+{1\over 2}\Delta t,y_n +{1\over 2}k_1,z_n+{1\over 2}j_1)$	(25)

$\displaystyle k_3$	$\textstyle =$	$\displaystyle \Delta t f(t_n+{1\over 2}\Delta t,y_n +{1\over 2}k_2,z_n+{1\over 2}j_2)$
$\displaystyle j_3$	$\textstyle =$	$\displaystyle \Delta t g(t_n+{1\over 2}\Delta t,y_n +{1\over 2}k_2,z_n+{1\over 2}j_2)$	(26)

$\displaystyle k_4$	$\textstyle =$	$\displaystyle \Delta t f(t_n+\Delta t,y_n+k_3,z_n+j_3)$
$\displaystyle j_4$	$\textstyle =$	$\displaystyle \Delta t g(t_n+\Delta t,y_n+k_3,z_n+j_3)$	(27)

練習問題4

式(28)で与えられる連立微分方程式を解け．なお，ω=とせよ．t=0.D0でvx=0.D0, vy=1.D0とする．

$\displaystyle {dv_x\over dt}$	$\textstyle =$	$\displaystyle f(t,v_x,v_y)=\omega v_y$
$\displaystyle {dv_y\over dt}$	$\textstyle =$	$\displaystyle g(t,v_x,v_y)=-\omega v_x$	(28)

$\displaystyle \lambda_1+\lambda_2$	$\textstyle =$	$\displaystyle 1$	(12)
$\displaystyle \lambda_1\alpha$	$\textstyle =$	$\displaystyle {1\over 2}$	(13)
$\displaystyle \lambda_2\beta$	$\textstyle =$	$\displaystyle {1\over 2}$	(14)

数値解析法及び演習 第八回