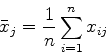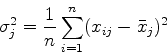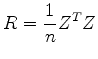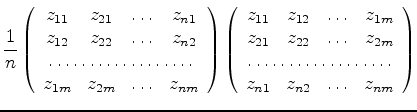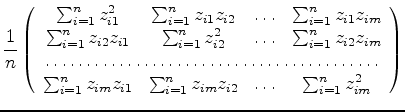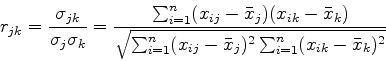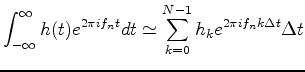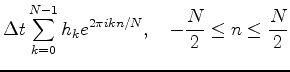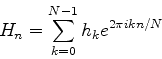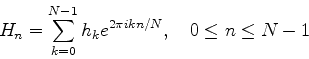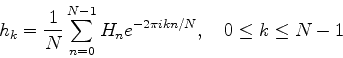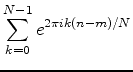数値解析法及び演習 第十三回

多変量の相関とフーリエ解析
  1. 多変量の相関
  2. フーリエ変換の復習
  3. 離散フーリエ変換
  4. 今日の宿題

[1] 多変量の相関

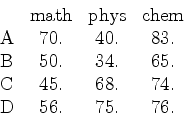
いくつかの特性に対するデータが得られたときそれをどう味わうかを考える． ここでは多変量の相関を考える．例として以下のデータをみてみよう．


\begin{displaymath} \begin{array}{cccc} & {\rm math} & {\rm phys}& {\rm chem} \... ... C} & 45. & 68. & 74.\\ {\rm D} & 56. & 75. & 76. \end{array}\end{displaymath} (1)

このように，サンプル(Aさん，Bさん．．)を行にとり，変量(数学，理科．．)を列 にとって作った測定値の行列をデータ行列と呼ぶ．多変量解析の目的は, どの変量とどの変量が相互に関係しているのかを統計的に推測することである.

一般に異なる変量は異なる次元を持つ．そのためまず各変量をおなじように扱 えるようにするために標準化という作業をおこなう．これは，平均値がゼロ， 分散が1となるような変換をデータに施すことである．ある変量の平均値は


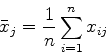\begin{displaymath} \bar{x}_j={1\over n}\sum_{i=1}^nx_{ij} \end{displaymath} (2)


であたえられる．分散（標準偏差の二乗）は


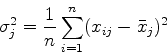\begin{displaymath} \sigma_j^2={1\over n}\sum_{i=1}^n(x_{ij}-\bar{x}_j)^2 \end{displaymath} (3)

となる．データの標準化は


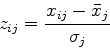\begin{displaymath} z_{ij}={x_{ij}-\bar{x}_j\over \sigma_j} \end{displaymath} (4)

の変換によっておこなわれる．この変換をおこなった行列を標準化行列と呼ぶ．標準化の結果, 平均値が0, 分散が1となる.


\begin{displaymath} Z= \left( \begin{array}{cccc} z_{11} & z_{12} & \ldots & z_{... ...fill}\\ z_{n1} & z_{n2} & \ldots & z_{nm} \end{array}\right) \end{displaymath} (5)

ここでこの行列の転置行列をかけると


$\displaystyle R={1\over n}Z^{T}Z$ $\textstyle =$ $\displaystyle {1\over n} \left( \begin{array}{cccc} z_{11} & z_{21} & \ldots & ... ...icolumn{4}{c}{\dotfill}\\ z_{n1} & z_{n2} & \ldots & z_{nm} \end{array}\right)$  
  $\textstyle =$ $\displaystyle {1\over n}\left( \begin{array}{cccc} \sum_{i=1}^{n} z_{i1}^2 & \s... ...um_{i=1}^{n} z_{im}z_{i2} & \ldots & \sum_{i=1}^{n} z_{im}^2 \end{array}\right)$ (6)

となり各要素は二つの変量の間の相関係数を与える．変量jと変量kの相関係数は


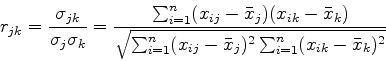\begin{displaymath} r_{jk}={\sigma_{jk}\over \sigma_j\sigma_k} ={\sum_{i=1}^n(x_... ..._{i=1}^n(x_{ij}-\bar{x}_j)^2\sum_{i=1}^n(x_{ik}-\bar{x}_k)^2}} \end{displaymath} (7)

であたえられる．二つの変量の相関がよいほど相関係数の値の絶対値は1に近 くなる．行列Rの要素はそれぞれ二つの変量の相関係数のため，Rは相関行列と 呼ばれる． それではでて来た相関係数はどう味わえばよいのか？ それには次の表を用いる. Nはデータの数, rは相関係数である. それぞれの数値は, 無相関のN個のデータがあった時にr以上の相関係数が出現する確率（パーセント）である. この数値が小さい程, 二つのデータには相関があると思ってよい. 5以下なら有意, 1以下なら高度に有意であるという.
r
N 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0
3 100 94 87 81 74 67 59 51 41 29 0
6 100 85 70 56 43 31 21 12 6 1 0
10 100 78 58 40 25 14 7 2 0.5 0
20 100 67 40 20 8 2 0.5 0.1 0
50 100 49 16 3 0.4 0

表１：無相関な二つの量がN組あったとき, 相関係数がr以上になる確率. 空白は0.05%以下.

練習問題1

14人の「健康診断データ」を用いて相関行列を作成せ よ．データは左から，年齢，最大血圧，最小血圧，大動脈脈波速度，血清総コ レステロール，の順に並んでいる．どの項目とどの項目が相関があるか指摘せよ．

アドバンスト練習問題

乱数を生成するアルゴリズムを用いて，表1を作成せよ．

[2] フーリエ変換の復習

フーリエ変換はさまざまな場面で出会うことになる. 地震の波形解析, 気候変動の解析, 地層の縞の解析などが典型的な例である. 今週と来週は離散データをフーリエ変換する手法を学ぶ. 今週は離散フーリエ変換のアルゴリズムを作成し, 来週はそれを用いる際の注意点および応用を学ぶ.

時間の関数h(t)が与えられたとしよう. h(t)のフーリエ変換, その逆変換は次式で与えられる. （注：一般には2πfではなくてωが用いられるが, ここでは計算の便利のため2πfを使う）


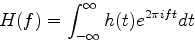\begin{displaymath} H(f)=\int^{\infty}_{-\infty}h(t)e^{2\pi ift}dt \end{displaymath} (8)


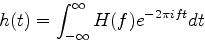\begin{displaymath} h(t)=\int^{\infty}_{-\infty}H(f)e^{-2\pi ift}dt \end{displaymath} (9)

フーリエ変換を行うと関数h(t)は関数H(f)に変換される. H(f)は一般に複素数となる. その絶対値の二乗は, 周波数f〜f+dfに含まれるパワーになる. したがって, フーリエ変換すると, どの周波数成分が卓越しているかが分かる事になる.

以下でフーリエ変換を議論するときは, 次の形式でデルタ関数を書いておくと都合がよい.


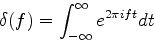\begin{displaymath} \delta (t)=\int_{-\infty}^{\infty}e^{2\pi i ft}dt \end{displaymath} (10)

練習問題2

式（１０）を用い, 式（８）から逆変換の式（９）を導け.

[3]離散フーリエ変換

我々が得るデータは普通離散データである. この場合, 一定の時間間隔Δtで物理量が計測される. 次の時刻tnについてN個のデータが得られているとしよう.


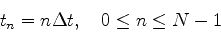\begin{displaymath} t_n={n\Delta t},\quad 0\le n\le N-1 \end{displaymath} (11)

Δtについて, ナイキストの臨界周波数という次式で定義される周波数が存在する.


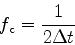\begin{displaymath} f_{\rm c}={1\over 2\Delta t} \end{displaymath} (12)

ナイキストの臨界周波数がなぜ重要かというと, この周波数以上の成分は正しくフーリエ変換されないためである. このため, 離散フーリエ変換をする時の周波数の上限が決まる.

ナイキストの臨界周波数の存在から, 離散フーリエ変換を行った場合に我々が得ることのできるフーリエ変換成分は-fcからfcまでであることが分かった. データがN個あるものとすると, このデータから得られるフーリエ変換成分もたかだかN個しかない. そこで次の値についてフーリエ変換を求めることにしよう.


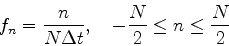\begin{displaymath} f_n={n\over N\Delta t},\quad -{N\over 2}\le n\le {N\over 2} \end{displaymath} (13)

式（８）を和で置き換えると以下のようになる.


$\displaystyle H(f_n)$ $\textstyle =$ $\displaystyle \int^{\infty}_{-\infty}h(t)e^{2\pi if_nt}dt\simeq \sum_{k=0}^{N-1}h_ke^{2\pi if_nk\Delta t}\Delta t$  
  $\textstyle =$ $\displaystyle \Delta t\sum_{k=0}^{N-1}h_ke^{2\pi i kn/N}, \quad -{N\over 2}\le n\le {N\over 2}$ (14)

一般に離散フーリエ変換は上式からΔtをとった


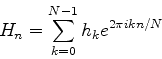\begin{displaymath} H_n=\sum_{k=0}^{N-1}h_ke^{2\pi i kn/N} \end{displaymath} (15)

を指す．このように定義しておくと次元によらずまた逆変換との対応もよく見える．

練習問題3

H-n=HN-nが成立している事を確認せよ.

上の問題から, H-n=HN-nであることが分かる. もともと式（１１ ）においてnは-N/2からN/2まで変化していたが, 0からN-1まで変化させることにしよう. こうすると, 0からN/2までは周波数0からfcまで対応し, N/2からN-1までは周波数-fcから-1/NΔtまでが対応することになる. すると最終的に求めるべき離散フーリエ変換は次式となる.


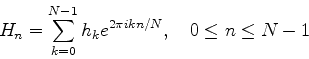\begin{displaymath} H_n=\sum_{k=0}^{N-1}h_ke^{2\pi i kn/N}, \quad 0\le n\le N-1 \end{displaymath} (16)

n番めの周波数のパワーは絶対値の二乗


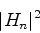\begin{displaymath} \vert H_n\vert^2 \end{displaymath} (17)

で与えられる．もとの関数が実数である場合には，周波数fと周波数-fのパワーは一致することに注意．

また, 離散逆フーリエ変換は次式で与えられる.


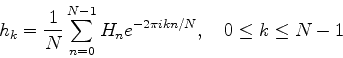\begin{displaymath} h_k={1\over N}\sum_{n=0}^{N-1}H_ne^{-2\pi i kn/N}, \quad 0\le n\le N-1 \end{displaymath} (18)

練習問題4


$\displaystyle \sum_{k=0}^{N-1}e^{2\pi i k(n-m)/N}$ $\textstyle =$ $\displaystyle N \quad n=m$  
  $\textstyle =$ $\displaystyle 0 \quad {\rm else}$ (19)

を用いて, 式（１６）から離散逆フーリエ変換の式（１８）を導け.

今日の宿題 (1/20日まで)

１）式（１６）を元に, 離散フーリエ変換を行うアルゴリズムを作成せよ. もとのデータは実数とする.

２）式（１８）を元に, 離散フーリエ変換の結果を逆変換するアルゴリズムを作成せよ.

３）このデータは, 時間間隔 0.209439(=2π/30)，時間領域 0< t < 2π においてある関数をサンプリングしたものである．ある関数とは３つの正弦波の和である．どのような振動数の正弦波が含まれているか作成したアルゴリズムを用いて算出せよ．得られた結果を逆変換し, 元のデータに戻ることを確かめよ.

それでは，実際に得られたデータのフーリエ変換を行ってみる．データに含まれている強い波の周期を読みとってみよ．

プログラムと３）の結果（３つの周波数）および，上のデータに含まれる強い周期（年）を送ること（n=0の成分は除く）. その周期は地球の軌道変化の周期と関連していると言われている．


日程表へ戻る <<