Lesson 2. 「波素」とAR過程

　　存否法は、複雑な波形データを「波素（なみそ）」に分解することを目標とします。「波素｣とは、以下の四つのパラメータ一組で定義される単純な波です。

＊ｆ：周波数 frequency

＊g：成長率 growing rate

＊c：初期振幅 initial amplitude

＊φ：初期位相 initial phase

この四つのパラメータでもって、一つの波素は以下のように定義されます。

u(t) = c exp(gt) cos(2πft+φ)　　　　　　　（１）

gが正の場合は振幅が時間とともに増大する正弦波を表し、負の場合は減衰する正弦波を表します。

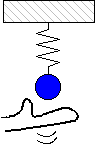
　　ここで、下のようなばね振り子の運動を考えてみましょう。

おもりを手でポンとたたいてやると、おもりは振動をはじめます。おもりの変位 u(t) を観測するとして、おもりの運動方程式は以下のようになります。

m d²u/dt² + η du/dt + k u = 0　　　　　　（２）

mはおもりの質量、ηは抵抗力の係数、kはばね定数です。この運動方程式の解は、振幅が指数関数的に減衰する正弦波となり、すなわち（１）式のような波素の形をしています。

　ここで、おもりの変位u(t)をあるサンプリング間隔で観測して、離散時系列データが得られるとしましょう。以下、時間の単位をサンプリング間隔にとります。上の運動方程式を、データにあわせるように離散化しましょう。すなわち、

du/dt →　u(t)-u(t-1)

などのように置き換えてやると、

a₁u(t+1) + a₀u(t) + a_-1u(t-1) = 0　　　　　　（３）

となります。ここで { a_j } はm､η､kなどで表される定数で、ばね振り子の特性を表現する数値の組になります。

　　おもりとばねがたくさんつながったような複雑な振り子の運動の場合には、離散化した運動方程式は（３）式を一般化して

　Σ_j=-M^M a_j u(t-j) = 0　　　　　　　　　　　　　（４）

と表すことができます。このような形の方程式で表される過程を（ばね振り子に限らず）自己回帰過程（AR過程）と呼びます。数列 { a_j }は対象にしている力学系の特性を表すパラメータでＡＲ係数と呼び、その(個数−１)/2= M をＡＲ次数と呼びます。（４）式の解は（１）のような波素が複数重ねあわされたものになります。すなわち、

　u(t) = Σ_j=-M^Mc_ｊ exp(g_ｊt) cos(2πf_ｊt+φ_ｊ)　　（５）

で、ＡＲ次数×2の2M 個の波素の重ねあわせとなります。