第一問(10点)
第10回におこなったケプラー問題の運動方程式に,速度に比例する抵抗力を追加する.
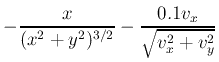 |
|||
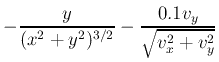 |
(1) |
この式で右辺第二項が抵抗力である.0.1は,ゆっくり減速させるためにかけてある.初期座標 x=1.D0, y=0.D0, 初速 vx=0.D0, vy=1.D0 とし,dt=1.D-2とする.原点からの距離が0.1よりも小さくなるまでに,質点は中心の周りを何周するか? 1周に満たない分は切り捨てること.
プログラムおよび,周回数の値(整数)を送付すること.第10回におこなったケプラー問題の運動方程式に,速度に比例する抵抗力を追加する.
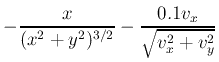 |
|||
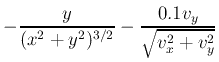 |
(1) |
この式で右辺第二項が抵抗力である.0.1は,ゆっくり減速させるためにかけてある.初期座標 x=1.D0, y=0.D0, 初速 vx=0.D0, vy=1.D0 とし,dt=1.D-2とする.原点からの距離が0.1よりも小さくなるまでに,質点は中心の周りを何周するか? 1周に満たない分は切り捨てること.
プログラムおよび,周回数の値(整数)を送付すること.台形公式を用いて次の積分を数値的に求めよ.Δx=1.D-2,a=1.D1 として値を求めること.
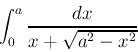 |
(2) |
第12回の課題「波動方程式」において,初期条件を下式で与える.固定端を用いて計算を行う.初速度はゼロとする.始めに,左から右に向かって波が進行する.波の頂点のx座標を算出し,横軸を時間,縦軸を頂点の座標でグラフを描く.頂点の座標が,c = 1 の速度で右に移動していることを確認せよ.
| (3) |
中心が (0.5, 0.5) にあり,半径が0.5の球の体積を乱数を用いて求めたい.0.0から1.0までの乱数を三回発生させ,1個目をx座標, 2個目をy座標,3個目をz座標とする.これをN回繰り返す.こうやって座標を生成すると,一片が1の立方体の中に満遍なく座標が分布するはずである.一方で,それぞれの座標が球の中に入ったか外側かを判定することができる.