数値解析法及び演習第十五回

第一問（10点）

次の運動方程式をルンゲクッタ法を用いて数値的に解け．t=0.D0　で　dx/dt=1.D0, x = 0.D0, タイムステップdt=1.D-1 とする．横軸x,　縦軸yでgnuplotでグラフを描画すること．xの最大値と，その時のtをプログラムと共に送付せよ．

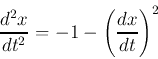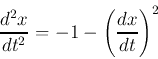$\begin{displaymath} {d^2x\over dt^2}=-1-\left({dx\over dt}\right)^2 \end{displaymath}$

(1)

プログラムおよび，xの最大値とその時のtの値を送付すること．

台形公式を用いて次の積分を数値的に求めよ．Δx=1.D-2として値を求めること．

$\begin{displaymath} \int_{0}^{1}\sqrt{x(1-x)}dx \end{displaymath}$

(2)

プログラムと数値を送付すること．

このデータは，800体のポケモンのデータである(https://www.kaggle.com/rounakbanik/pokemonより)．左から順にattack, base_total, capture_rate, defense, hp, speed　の数値が並んでいる．

プログラムと答え（1:相関係数の最大値とデータの名前　2：寄与率2つ）を送ること．

20名の学生からなるクラスが100ある．乱数を用いて，誕生日が同じ学生が少なくとも1組存在するクラスの数を求めよ．一年は365日とする．

プログラムと，誕生日が同じ学生がいるクラスの数を送付すること．