数値解析法及び演習第十五回

第一問（10点）

ルンゲクッタ法を用い，次の一階連立常微分方程式を，初期条件t=0でx=1.D0, y=-1.D0で解きなさい．dt=1.D-2でt=2まで積分すること．

$\displaystyle {dx\over dt}$	$\textstyle =$	$\displaystyle 3x-y$
$\displaystyle {dy\over dt}$	$\textstyle =$	$\displaystyle x+y$	(1)

プログラムと，t=2におけるx,yの値を送ること．

第二問（10点）

次の積分を台形公式を用いて数値的に求めよ．積分区間を100分割すること．

$\begin{displaymath} \int_0^1 \sqrt{(x(1-x))} \end{displaymath}$

(2)

プログラムと解の値を送付すること．

第三問（10点）

第12回の講義（1/12）において配布した，月の鉄量（FeO量）マップデータ（FeO_720x360.raw）を用いて下記の問いに答えよ．

月の海（月の黒っぽい領域）を構成している玄武岩は，月の高地（月の白っぽい領域）を構成している斜長岩に比べて鉄量が高い．ここで，鉄量が10 wt%以上の領域を海の領域，10 wt%未満の領域を高地の領域と定義する．鉄量（FeO量）マップデータを用いて，月面を海領域と高地領域に分類し，海領域には”2”の値を，高地領域には”1”の値を格納したバイナリデータを出力するプログラムを作成しなさい．

出力するファイルは，1ピクセルあたりのバイト数を2バイト (16bit)，画像サイズを入力データと同じ，720 (横) x 360 (縦)とすること．

（注意）入力データの値の単位は [wt%] であり，ファイルにはその100倍の値が格納されている．
プログラムを送ること．

第四問（10点）

問題1：

0から1までの値をとる2つの乱数(x1,x2)をN回発生させる．

$\begin{displaymath} x_1^2+x_2^2\le 1 \end{displaymath}$

(3)

を満たした乱数の組をN2とし，N2/Nを四倍することで半径1の円の面積を近似的に求めよ．四倍する理由は，式を満たす条件は第一象限の扇形の面積だけに相当するからである．N=10000として答えを求めよ．

問題2：

0から1までの値をとるM個の乱数(x1, x2, ... xM)をN回発生させる．

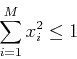$\begin{displaymath} \sum_{i=1}^{M}x_i^2\le 1 \end{displaymath}$

(4)

を満たした乱数の組をN2とすると，N2/Nを2**M倍することで半径1のM次元球の体積を近似的に求めることができる．この体積はあるMで最大値をとる．そのMと最大値を求めよ．N=1000000とせよ．

プログラムと答えの数値をそれぞれ送付すること．

数値解析法及び演習 第十五回

第一問（10点）

第二問（10点）

第三問（10点）

第四問（10点）

第五問（2点）

数値解析法及び演習第十五回