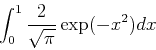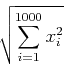数値解析法及び演習第十五回

第一問（10点）

次の二階常微分方程式を，初期条件t=0でx=2.D0, dx/dt=0.D0で解くことを考える．

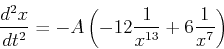$\begin{displaymath} {d^2x\over dt^2}=-A\left(-12{1\over x^{13}}+6{1\over x^7}\right) \end{displaymath}$

(1)

問題1:

x=2では右辺は負となるので，始めはxは小さくなる．その後どこかのxで右辺はゼロとなり，それよりもxが小さくなると右辺は正となる．右辺がゼロとなる座標を解析的（手で計算して）に求めよ．

問題2:

ルンゲクッタ法を用いてプログラムを作成し，横軸t,　縦軸xのグラフを作成する．異なるAの値を用いて計算を何回か行う．x=2の位置まで戻って来るのにかかる時間はAの何乗に比例するか？

プログラムと１，２の答えの数値を送ること．

第二問（10点）

次の積分を台形公式を用いて数値的に求めよ．積分区間を100分割すること．

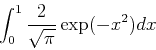$\begin{displaymath} \int_0^1 {2\over \sqrt{\pi}}\exp(-x^2) dx \end{displaymath}$

(2)

プログラムと解の値を送付すること．

第三問（10点）

次の月の地殻厚データを用いて，各経度における赤道の地殻厚を算出し，最大値とその経度を算出せよ．地殻厚データは，緯度方向は-89.75 度を始点として0.5 度おき（180度÷360pixel=0.5度/pixel）に89.75 度まで，経度方向には 0.25 度から0.5 度おき（360度÷720pixel=0.5度/pixel）に359.75 度までのデータとなっている．ここでは緯度-0.25 度と0.25 度の値の平均を赤道の値とする．

月周回衛星「かぐや」全球地殻厚マップデータ
ファイル名：crust-basalt_mac_720x360.raw
バイト数：2 (16 bit)
画像サイズ：720 (横) x 360 (縦) x 1 (バンド数)
ヘッダーサイズ：0
バイト順序：intel
第11回の講義（2015/12/17）に配布済み．またはこちらよりダウンロード可能．
プログラムと答え（地殻厚の最大値，その経度）を送ること．

第四問（10点）

問題１：

１次元のランダムウォークを考える．各タイムステップ毎に0から1までの乱数を振って0.5よりも小さければ-1, 大きければ+1だけ球がx軸上を移動する．1000個の球を考え，すべての球は始めはx=0にいるものとする．プログラムを作成し，次の和がタイムステップ数の何乗に比例して増加するか答えよ．

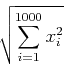$\begin{displaymath} \sqrt{\sum_{i=1}^{1000}x_i^2} \end{displaymath}$

(3)

問題２：

前問において，タイムステップ10回につき1回，もしx>0ならx=x-1, x<0ならx=x+1と球の位置を強制的に移動させたとする．その場合に上の和はどのように時間進化するか答えよ．

プログラムと答えの数値（問題１），文章（問題２）を送付すること．

数値解析法及び演習 第十五回

第一問（10点）

第二問（10点）

第三問（10点）

第四問（10点）

第五問（2点）

数値解析法及び演習第十五回