数値解析法及び演習第八回

[1] 文字処理

[1.1] 文字定数

アポストロフィ(')で挟まれた文字列を文字定数という. 例：'hoge'

[1.2] 文字型の宣言

文字定数を格納するためには「文字型」の変数を宣言する必要がある.

a,b,c	変数, 配列, 関数副プログラム名
文字型宣言文	character a10, b(2,2)5,c
10, 5	文字数の指定

例：

       implicit none
       character a*5

       a='hoge'
       write(6,*) a
       end

[1.3] 連結

スラッシュを二つ(//)書くことで文字型変数や定数を連結することができる.

例：

       implicit none
       character a*5,b*10

       a='hoge'
       b=a//'hoge'
       write(6,*) b
       end

[1.4] 文字列の位置

文字列の一部を指定することができる. a(m:n)によって変数aの第m文字目からn文字目を表す. 配列の場合, a(k)(m:n)とすると, k番目の配列要素のm文字目からn文字目を指定する.

例：

       implicit none
       character x*10,y*4,z(3)*5
       x='0123456789'
       y=x(3:6)
       z(1)(3:5)=x(1:3)
       write(6,*) x,' ',y,' ',z(1)
       end

[1.5] 文字型の組み込み関数

char(整数)	整数値を文字に変換. I=0～255の値から, その値に対応する文字に変換する.
関数名	意味
ichar(文字型変数, もしくは文字定数)	文字をコード表に対応する整数値に変換.
index(a,b)	文字列a中にある文字列bの位置（整数）. 文字列bが見付からない場合は0を返す.
len(文字型変数, もしくは文字定数)	文字列aの長さ（整数）.

例：

      implicit none
      character a*10,b
      integer n,m,k

      a='abcdefghi'

      b=char(100)
      n=ichar('d')
      m=index(a,'de')
      k=len(a)
      
      write(6,*) b,n,m,k

      end

[1.6] 文字, 文字列の大小関係

文字と整数値との間にはコード表によって対応関係がある. この整数値を用いて異なる文字の間の大小関係を定める. 比較には.eq., .ne., .gt., .ge., .lt., .le.を用いる.

例：

      implicit none
      character a,b

      a='c'
      b='c'

      if(a.eq.b) write(6,*) a,b

      end

同様にして, 文字列の大小の比較が行われる. 文字列の先頭の文字が異なる場合, それらの文字同士の大小で文字列の大小を定める. 先頭の文字が同じ場合, 二文字目以降で最初に異なる文字の大小で大小関係を定める. 文字列の長さが異なる場合, 短い方の文字列の後ろに空白文字を付け加えて比較する. 空白文字の整数値は32で, どの英数字よりも小さい.

例： ABA□□ < ABC□□ < ABCDE

練習問題1

char()関数を用い, 0から127（＝2の7乗）に対応する全ての文字をモニタに出力させよ.
キーボードから10文字以内の文字を入力し, その中に含まれる小文字の数をカウントするプログラムを作成せよ.
小文字で英単語を一つキーボードから入力し, 頭の文字のみ大文字に変換してモニタに表示するプログラムを作成せよ.

[2] 数の表現

[2.1] 整数の内部表現

練習問題2

2進数での1011は10進数だといくつ？

計算機はミクロにはon,offの2状態しか扱うことができない. したがって計算機が計算している「数」は実際にはすべて2進数である. そこで計算機の内部で数がどう表されているか考えてみよう. ここではまず整数を考える.

簡単のために3ビットの計算機を考えよう. つまりこの計算機で取り扱えるのは3個の0, 1 の組である. 3ビット計算機は次の表に表されるように整数を取り扱う.

整数の内部表現（3ビット計算機）
符合のための1bit	数値のための2bits	表される整数
0	11	3
0	10	2
0	01	1
0	00	0
1	11	-1（1に対する2の補数）
1	10	-2（2に対する2の補数）
1	01	-3（3に対する2の補数）
1	00	-4=2の（3-1）乗

この表から推測されるように, nビット計算機で取り扱える数は2の(n-1)乗-1 からマイナス2の(n-1)乗までとなる. 次のプログラムを実行してみよ.

      implicit none
      integer n,m,k
      n=2147483647
      m=n+1
      k=m+n+1
      write(6,*) n,m,k
      end

このプログラムはどうなるであろうか？

      implicit none
      integer n,m,k
      n=2147483648
      m=n+1
      k=m+n+1
      write(6,*) n,m,k
      end

[2.2] 実数の内部表現

現在流通している多くのコンピューターは32ビット計算機である．これは，内部で扱う数値を32個の0と1で表現しているということである．

単精度実数の内部表現（32ビット計算機）
仮数部の符号1bit	指数部の8bits	仮数部（23bits）
0	00000000	00000000000000000000000

倍精度実数の内部表現（32ビット計算機）
仮数部の符号1bit	指数部の11bits	仮数部（52bits）
0	00000000000	00000000000000000000000..

1bitはプラスかマイナスの符号につかう．8bitsを指数部に使う（倍精度の場合11bits）．8個の0と1で-126から＋127までの数を表す（倍精度の場合-1022から1023まで）. ここからフォートランで用いることができる数値は2の127乗=10の38乗まで（倍精度の場合10の308乗まで）ということになる．広く採用されているIEEE規格では基数を2ととることに注意．

残りの23個（倍精度の場合52個）を使って仮数部(0.234E5 だったら 0.234の部分)を表す．小数第1桁目は1ときまっているので表現はしないため実質2進数で24桁（倍精度の場合53桁）ということになる. 24桁なので仮数部で表せるもっとも小さな数は2の-24乗=0.6*10^(-7)（倍精度の場合0.1*10^(-15)）となる．このことから数値的な誤差が発生する．次のプログラムを実行させてみよう．

      implicit none
      real*8 a,b,c,d,e
      a=1.D-15
      b=1.D-16
      c=1.D0
      d=c+a
      e=c+b
      write(6,"(3E26.18)") a,b,c,d,e
      end

結果はどうなったであろうか? これが誤差を生み出す原因である．ここで見られる誤差は二つあって

丸め誤差：数を2進数で表現しようとするため発生する誤差．0.999999999999999979E-16がそれにあたる．
情報落ち誤差：桁が違う数を足し算，引き算することにより発生する誤差．1.D0+1.D-16が1.D0になってしまう誤差．

である．

[3] 台形公式

関数f(x)のある区間[x0, xn]の積分を考える．この区間をn個に分割すると積分は

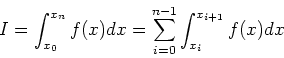$\begin{displaymath} I=\int_{x_0}^{x_n}f(x)dx=\sum_{i=0}^{n-1}\int_{x_i}^{x_{i+1}}f(x)dx \end{displaymath}$

(3)

となる．ここでf(x)よりも下の面積を台形で近似すると

$\begin{displaymath} \int_{x_i}^{x_{i+1}}f(x)dx={h\over 2}(f(x_i)+f(x_{i+1})) \end{displaymath}$

(4)

となる．ここから, 求めたかった積分は次のように書ける.

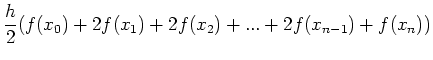$\displaystyle I$	$\textstyle =$	$\displaystyle {h\over 2}(f(x_0)+2f(x_1)+2f(x_2)+...+2f(x_{n-1})+f(x_n))$
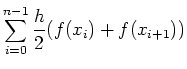	$\textstyle =$	$\displaystyle \sum_{i=0}^{n-1}{h\over 2}(f(x_i)+f(x_{i+1}))$	(5)

練習問題3

$\begin{displaymath} I=\int_{0}^{1}e^xdx=e-1=1.718281828... \end{displaymath}$

(6)

を台形公式により求めよ．区間の分割の数nを10，100，1000，．．．と変化させ，誤差がどう変化するか観察せよ．またなぜそのnで誤差が変化するのか考察せよ．

[4] シンプソン公式

シンプソン公式は，台形公式の精度をあげたものである．台形公式の精度を計算すると，幅Δxの2乗に比例することを示すことができる．
台形公式ではf(x)上の二つの点を直線でむすんだ．よりよく数値積分を行うためには次の精度，つまりf(x)を二次曲線で近似すればよい．台形公式では2 点を用いることで直線を決定した．なので今度は3点を用いれば二次曲線を決定することができる．シンプソン公式は, 誤差がΔxの4乗に比例する.
並んだ二つの区間x1-x2,x2-x3を考える．それぞれ関数fの値はf1,f2,f3とする．この区間において関数fが二次式

$\begin{displaymath} f(x)=ax^2+bx+c \end{displaymath}$

(8)

であったとすると，この区間の積分は次になることを示すことができる．

$\begin{displaymath} \int_{x_1}^{x_3}f(x)dx={h\over 3}(f_1+4f_2+f_3) \end{displaymath}$

(9)

この等式を示すにはまず, 式（8）の積分を行なうと

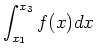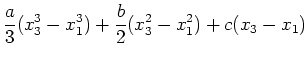$\displaystyle \int_{x_1}^{x_3}f(x)dx$	$\textstyle =$	$\displaystyle {a\over 3}(x_3^3-x_1^3)+{b\over 2}(x_3^2-x_1^2)+c(x_3-x_ 1)$
	$\textstyle =$	$\displaystyle (x_3-x_1)\left[{a\over 3}(x_1^2+x_1x_3+x_3^2)+{b\over 2}(x_1+x_3)+c\right]$	(10)

一方, 式（9）の右辺を計算すると

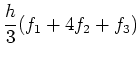$\displaystyle {h\over 3}(f_1+4f_2+f_3)$	$\textstyle =$	$\displaystyle a(x_1^2+4x_2^2+x_3^2)+b(x_1+4x_2+x_3)+c(1+4+1)$
	$\textstyle =$	$\displaystyle 2h[{a\over 3}(x_1^2+x_1x_3+x_3^2)+{b\over 2}(x_1+x_3)+c]$	(11)

x3-x1=2hであるのでこれら二式は等しいことがわかる.

練習問題4

シンプソン公式を用い，先ほど台形公式を用いて計算した積分を行い，台形公式の場合と結果を比較せよ．積分区間を10, 100, 1000等分して誤差を比較すること．

[5] 今日の宿題

練習問題1の第3問のプログラム＋練習問題4のプログラムを結果と共に送ること. 〆切は12/14.

日程表へ戻る << 　

数値解析法及び演習 第八回