数値解析法及び演習第十五回

第一問（15点）

次の微分方程式をルンゲクッタ法を用いて数値的に解け．初期条件はt=0.D0でx=1.D0, dx/dt=0.D0とする．dt=1.D-1とし，t=100.D0まで計算すること．＜プログラム＞

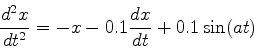
$\begin{displaymath} {d^2x\over dt^2}=-x-0.1{dx\over dt}+0.1\sin(at) \end{displaymath}$ (1)
a=1.D0とa=2.D0の場合で結果はどう異なるか？　またそれはなぜか？＜答え＞

第二問（10点）

このデータは，古い1000フランのスイス紙幣についてのものである（http://sun.econ.seikei.ac.jp/~shinmura/archive.html　より引用）．データは左列から順に，紙幣の長さ，紙幣の左側の高さ，右側の高さ，下側の余白の幅，上側の余白の幅，印刷部の対角線の長さと並んでいる．以前（12月10日）に作成したプログラムを用いて，各量の間の相関係数を算出せよ＜プログラム＞．どの量とどの量との間にもっとも相関が認められるか答えよ＜答え＞．

第三問（10点）

方程式の根　(f(x)=0を満たすようなx)を求めるプログラムを以下の手順で作成せよ．根xはx_L< x < x_Rの範囲にあることは既知であるとする．

x_M=(x_L+x_R)/2を計算する
f(x_L)*f(x_M)>0ならx_L=x_M，f(x_L)*f(x_M)≤0ならx_R=x_Mとする．
上記を繰り返す．dabs(x_R-x_L)≤ e となったら終了．eは許容する誤差である．

このプログラムを用いて，

$\begin{displaymath} f(x)=x^3-2x^2-5x+6=0 \end{displaymath}$

(2)

の3つの根を求めよ＜プログラム＞＜答え＞．e=1.D-5とせよ．計算の前にgnuplot で関数f(x)をプロットし，大体の根の値を見つけた上でx_R, x_Lを設定すること．

数値解析法及び演習 第十五回

第一問（15点）

第二問（10点）

第三問（10点）

第四問（5点）

数値解析法及び演習第十五回