数値解析法及び演習 第十回

熱伝導方程式
  1. 熱伝導方程式を解くアルゴリズム（陰解法）
  2. 今日の宿題

[1]熱伝導方程式を解くアルゴリズム（陰解法）

一次元の熱伝導方程式を解くアルゴリズムを作成しよう．媒質が0からXまで広がっているとする. 温度分布の進化を決定する方程式は熱伝導方程式であり


\begin{displaymath} {\partial T\over \partial t}=\kappa {\partial^2 T\over \partial x^2} \end{displaymath} (1)

で与えられる. この偏微分方程式を解くためには初期温度分布と境界条件が必要となる. 初期温度分布は
\begin{displaymath} T(t=0,x)=T(x) \end{displaymath} (2)

で与える. 境界条件として今回は, 両端の温度一定の条件を与える.
$\displaystyle T(t,x=0)$ $\textstyle =$ $\displaystyle T(x=0)$ (3)
$\displaystyle T(t,x=X)$ $\textstyle =$ $\displaystyle T(x=X)$ (4)

基礎方程式を差分化しよう. 時間はΔt秒ごとに進むとしよう. 整数１で表わされた量は現在の値（これは既知；以下のT(1,k), kは空間座標を示す）, 整数２で表わした量はΔt秒後のもの（求めるべき未知の量；T(2,k)）とする. 空間は幅ΔxでN-1分割する. そうすると空間方向にはN個のグリッドがあることになる. 空間を整数kで表すと1&le k&le Nとなる. 熱伝導方程式の左辺は次のようになる.
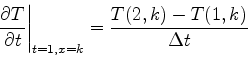\begin{displaymath} \left.{\partial T\over \partial t}\right\vert _{t=1,x=k}={T(2,k)-T(1,k)\over \Delta t} \end{displaymath} (5)

同様に右辺を差分化しよう. 場所に関する一次の微分は


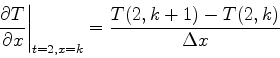\begin{displaymath} \left.{\partial T\over \partial x}\right\vert _{t=2,x=k}={T(2,k+1)-T(2,k)\over \Delta x} \end{displaymath} (6)

となる. 式(6)から, (6)にk-1を代入したものの引き算をすることで次のように二次微分を求めることができる．


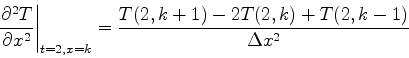\begin{displaymath} \left.{\partial^2 T\over \partial x^2}\right\vert _{t=2,x=k}={T(2,k+1)-2T(2,k)+T(2,k-1)\over \Delta x^2} \end{displaymath} (7)

ここで, 1ステップ進んでいる時刻２をとっている事に注意. これが陰解法のポイントである. 式(5)と(7)から, 差分化された熱伝導方程式は


\begin{displaymath} {T(2,k)-T(1,k)\over \Delta t}=\kappa{T(2,k+1)-2T(2,k)+T(2,k-1)\over \Delta x^2} \end{displaymath} (8)

となる. この式を書き換えると


\begin{displaymath} -AT(2,k+1)+BT(2,k)-CT(2,k-1)=T(1,k) \end{displaymath} (9)


\begin{displaymath} A=C=\kappa{\Delta t \over \Delta x^2} \end{displaymath} (10)


\begin{displaymath} B=1+2\kappa{\Delta t \over \Delta x^2} \end{displaymath} (11)

となることがわかる. A, B, Cはすべてわかっている量なので, 式(9)から作られる連立方程式(N-2本あることに注意）を解けば時刻２における温度がわかる事になる. しかし正直に解く必要は必ずしもない. 次のようにすればわざわざ計算しなくとも問題は解ける.
まず, 温度が次のように書けるものと仮定する.


\begin{displaymath} T(2,k)=E(k)T(2,k+1)+F(k) \end{displaymath} (12)

すると場所k-1においては
\begin{displaymath} T(2,k-1)=E(k-1)T(2,k)+F(k-1) \end{displaymath} (13)

となる. これら二式を式(9)に代入すると
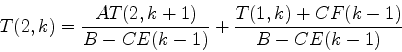\begin{displaymath} T(2,k)={AT(2,k+1)\over B-CE(k-1)}+{T(1,k)+CF(k-1)\over B-CE(k-1)} \end{displaymath} (14)

と書ける. これと式(12)を比較すると


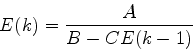\begin{displaymath} E(k)={A\over B-CE(k-1)} \end{displaymath} (15)


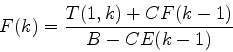\begin{displaymath} F(k)={T(1,k)+CF(k-1)\over B-CE(k-1)} \end{displaymath} (16)

となっていることがわかる.
式(12)においてk=1の場合について考えてみよう. k=1を代入すると


\begin{displaymath} T(2,1)=E(1)T(2,2)+F(1) \end{displaymath} (17)

となる. T(2,1)は境界条件で与えられていることに注意しよう. この式がT(2,2)の値によらずいつでも成立するためには


$\displaystyle E(1)$ $\textstyle =$ $\displaystyle 0$ (18)
$\displaystyle F(1)$ $\textstyle =$ $\displaystyle T(2,1)$ (19)

でないとダメなことがわかる. これでk=1におけるE, Fがわかった. これがわかれば, 式(15), (16)でk=2から順にE(N-1), F(N-1)まですべてのE, Fを求めることができる.

式(12)のkにN-1を代入すると


\begin{displaymath} T(2,N-1)=E(N-1)T(2,N)+F(N-1) \end{displaymath} (20)

となる．ここでT(2,N)は境界条件で既知であり，E(N-1),F(N-1) は先ほど求めているのでこの式からT(2,N-1)がわかる．次にこのT(2,N-1)と既知であるE(N-2), F(N-2)を用いることでT(2,N-2)がわかる．．．という具合にT(2,2)まで算出することができる．

[2] 今日の宿題 (12/9日まで)

作成したアルゴリズムを用いて，初期温度分布


\begin{displaymath} T(t=0,x)=0 \end{displaymath} (21)

境界条件


\begin{displaymath} T(t,0)=0\quad x=0 \end{displaymath} (22)


\begin{displaymath} T(t,0)=1\quad x=1 \end{displaymath} (23)

の場合の温度分布進化を求めよ．κ=1, Δt=1.D-3, Δx=1.D-2とし，t=1まで積分せよ．温度がちょうど0.5になっている場所


\begin{displaymath} T(t,x_{0.5})=0.5 \end{displaymath} (24)

は時間とともにどう移動していくか求めよ．

宿題もできた人のための課題

今までは，境界で温度を与える境界条件（ディリクレ条件）を与えていた．境界条件としては温度の微係数を与える（ノイマン条件）ことも考えられる．次の二つの境界条件で温度分布進化を求めよ．初期条件は今までと同じとする．温度が半分になっている場所の進化は求めなくてよい．

境界条件１


$\displaystyle {\partial T\over \partial x}$ $\textstyle =$ $\displaystyle 1 \quad x=1$ (25)
$\displaystyle T(t,0)$ $\textstyle =$ $\displaystyle 0\quad x=0$ (26)

境界条件２


$\displaystyle {\partial T\over \partial x}$ $\textstyle =$ $\displaystyle 1 \quad x=1$ (27)
$\displaystyle {\partial T\over \partial x}$ $\textstyle =$ $\displaystyle 0\quad x=0$ (28)




戻る <<