数値解析法及び演習 第十五回

テスト
  1. 16:00まで
  2. プログラム＋答えの数値をメールで送ること
  3. ひとつのメールにまとめて送付すること

第一問（15点）

次の連立方程式を数値的に解け．

プログラムと解の値を送付すること．


$\displaystyle x_1+x_2+x_3+x_4$ $\textstyle =$ $\displaystyle 1$ (1)
$\displaystyle 2x_1+5x_2-4x_3+x_4$ $\textstyle =$ $\displaystyle 5$ (2)
$\displaystyle 4x_1-x_2+7x_3+3x_4$ $\textstyle =$ $\displaystyle 0$ (3)
$\displaystyle 3x_1+x_2+x_3+2x_4$ $\textstyle =$ $\displaystyle 0$ (4)

第二問（10点）

次の二階常微分方程式を解くプログラムを作成せよ．初期条件t=0でx=1.D0, dx/dt=0.D0のもとで解き，t=4.D0におけるxを算出せよ．時間ステップ dt=1.D-1　とすること． プログラムとt=4.D0におけるxの値を送付すること．


\begin{displaymath} {d^2x(t)\over dt^2}+{dx(t)\over dt}+x(t)=0 \end{displaymath} (5)

第三問（10点）

次の積分をシンプソン則を用いて数値的に求めよ．積分区間を100分割すること．

プログラムと解の値を送付すること．


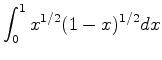$\displaystyle I_1$ $\textstyle =$ $\displaystyle \int_0^1x^{1/2}(1-x)^{1/2}dx$ (6)
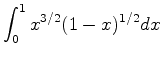$\displaystyle I_2$ $\textstyle =$ $\displaystyle \int_0^1x^{3/2}(1-x)^{1/2}dx$ (7)

第四問（5点）

40人の学生がいるクラスがある．このクラスに同じ誕生日の人が二人以上いる確率を求めよ．プログラムの考え方は概ね次のとおり

  1. 0から1までの乱数を発生させ，それを1から365までの乱数に変換する
  2. 上を40回行うと一つのクラスができたことになり，このデータを用いて同じ誕生日の人がいるかどうかチェックできる
  3. この作業を1000回行うことで確率を算出する
プログラムと確率の値を送付すること．

第五問（4点）




日程表へ戻る <<